고정 헤더 영역
상세 컨텐츠
본문
작성자 : 16기 윤지현
본 포스팅은 다음 자료들을 참고하여 작성되었습니다.
https://sdsclub.com/stochastic-gradient-descent-vs-gradient-descent-a-head-to-head-comparison/
1. Gradient Descent (=Batch-all training data set-Gradient Descent)
- loss function을 최소화하는 지점(미분 값, 즉 기울기가 0인 지점)을 찾는 것을 목적으로 한다.
- 단순히 방정식을 계산하는 것처럼 미분 값이 0인 지점을 구하는 것과는 무엇이 다른가 하는 의문에서 시작
- 실제로 다루는 loss function은 닫힌 형태가 아니거나 복잡한 형태를 가져 계산에 어려움 존재
《 원리 》
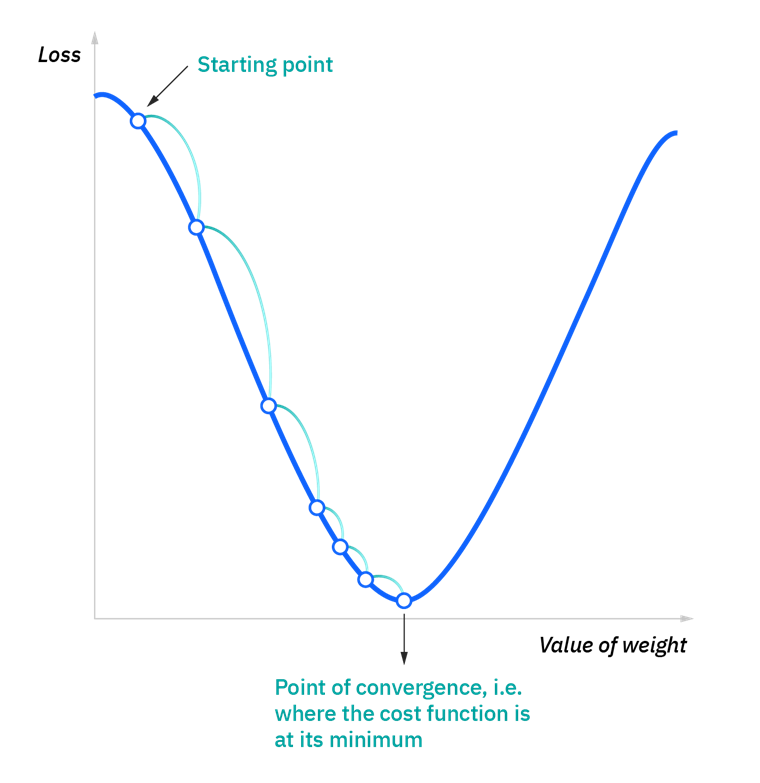
- loss function의 한 지점에 대해서 기울기 구한다.
- 기울기가 음수라면 해당 지점에서 오른쪽으로, 양수라면 왼쪽으로 이동
- 기울기의 절댓값이 클 경우 해당 지점에서 큰 폭으로 이동
- 기울기의 절댓값이 작아질수록 작은 폭으로 이동하며 기울기가 0이 되는 지점 탐색
모든 학습 데이터에 대해서 계산하기 때문에 어렵고 비생산적이라는 단점을 가진다.
→ 이를 해결하기 위한 ''Stochastic Gradient Descent'' 알고리즘
2. Stochastic Gradient Descent
- 모든 training data의 batch에 대해 계산하는 gradient descent와 달리, stochastic gradient descent의 batch size = 1로 해서 gradient를 계산한다.
▶ 장점

- 속도가 빠르다.
- 샘플이 큰 경우에도 사용이 가능하다.
- local minima에서 빠져나오기 쉽다.
▶ 단점
- soloution이 최적이 아닌 경우가 존재한다.
- optimal solution을 찾아가는 방향이 너무 뒤죽박죽이다.
→ 이를 해결하기 위한 "Stochastic Gradient Descent with Momentum" 알고리즘
3. Stochastic Gradient Descent with Momentum
- SGD(Stochastic Gradient Descent)에 관성(momentum)을 추가하여 최적화 solution을 찾는다.
《 원리 》
- 과거에 이동했던 방식을 기억하면서 그 방향으로 일정 정도 추가로 이동한다.
- SGD과 최적화 방법을 비교하면 뒤죽박죽의 정도가 덜하다.

4. Mini-Batch Gradient Descent
- 전체 데이터셋을 여러 개의 minibatch로 나누어, 각각의 minibatch 마다 기울기를 구하고 그것의 평균 기울기를 통해 모델을 업데이트한다.
- Gradient Descent와 SGD의 개념이 결합되어 있는 것으로 Gradient Descent의 효율성과 SGD의 내구성을 가진다.
▶ 장점
- Gradient Descent 보다 update를 자주하기 떄문에 더 강력한 수렴을 허용한다.
- local minima를 피할 수 있다.
- 전체 데이터셋이 아닌 일부 학습 데이터만 사용하기 때문에 메모리 사용량이 적다.
▶ 단점
- 알고리즘의 구현에 있어 minibatch_size 하이퍼파라미터를 추가로 설정해 주어야 한다.
- Gradient Descent보다는 메모리 사용이 적지만 error information을 minibatch 크기만큼 축적해서 계산해 주어야 하기 때문에 SGD 보다는 더 많은 메모리를 사용해야 한다.

5. AdaGrad
- learning rate decay(학습률 감소)를 사용하여 처음에는 크게 학습하다가 점점 작게 학습힌다.
- 각 매개변수에 adaptive하게 조정하여 맞춤형 learning rate를 설정한다.
《 원리 》

- 현재까지 변화가 적은 변수들은 step size를 크게, 변화가 많은 변수들은 step size를 작게한다.
- 변화가 많은 변수들은 optimum 근처에 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀하게 값을 조정한다.
- 변화가 적은 변수들은 optimum에 도달하기 위해서는 많이 이동해야 할 확률이 높기 때문에 빠르게 loss 값을 줄이는 방향으로 이동하려는 방식을 적용한다.
▶ 단점
- 갱신 정도가 약하기 때문에 무한히 학습한다면 갱신량이 0이 되어 학습 효과가 없다.
→ 이를 해결하기 위한 "RMS Prop & AdaDelta" 알고리즘
6. RMSProp & AdaDelta
《 RMSProp 》
- 과거의 기울기들을 똑같이 더해가는 것이 아니라 먼 과거의 기울기는 조금 반영하고 최신의 기울기를 많이 반영하면서 더해간다.
- 이를 exponentially weighted moving average(지수 가중 이동 평균)이라 한다.
《 AdaDelta 》
- RMSProp와 동일하게 AdaGrad의 단점을 보완하기 위해서 고안되었다.
- AdaGrad, RMSProp, Momentum의 특징을 모두 포함한 경사 하강법이다.
- AdaGrad의 특징인 모든 step의 gradient 제곱의 합을 window size로 두어 window size만큼의 합으로 변경하고, RMSProp와 같이 지수 이동 평균을 적용한다.
- second order methods를 사용하여 saddle point에서 문제가 발생하지 않지만, 상대적으로 계산 속도가 느리다.
7. Adam
- AdaGrad와 Momentum의 특징을 포함한 경사 하강법이다.
- 이전 learnig rate의 경향과 이전 gradient의 경향을 동시에 사용한다.
→ 가장 좋은 학습 성능을 가진다.
<전체 Optimization Algorithm 요약>


'심화 스터디 > Dive into Deep Learning' 카테고리의 다른 글
| [Dive into Deep Learning / CNN] CNN 구현해보기 (0) | 2022.11.21 |
|---|---|
| [Dive into Deep Learning / CNN] Convolution Layer (0) | 2022.11.18 |
| [Dive into Deep Learning / CNN] AlexNet (0) | 2022.11.16 |
| [Dive into Deep Learning / CNN] Fully connected layer / pooling layer (0) | 2022.11.13 |
| [Dive into Deep Learning / 3주차] Python Class (2) | 2022.09.30 |





댓글 영역