[Advanced ML & DL Week2] Zero-shot Learning Through Cross-Modal Transfer

작성자 : 14기 김태영

논문링크 : Zero-shot Learning Through Cross-Modal Transfer

---

1. Introduction

1) Zero-Shot Learning

 

 Zero-Shot Laerning이란 "unseen example에 대해서 문제를 잘 해결할 수 있도록 모델을 학습하는 것"을 의미한다.

일반적으로 딥러닝 모델들은 training에 사용된 class만을 예측할 수 있다.

 

 따라서 unseed example이 입력되더라도 내부 메커니즘에 의해 학습했던 seen class 중 하나로 예측하는 문제가 생기게 되는데 zero-shot learning은 이 때 train set에 포함되지 않는 unseen class를 예측하는 분야이다. 즉 다시 말하자면 unseen example을 입력받아도 seen data로 학습된 지식을 전이하여 unseen example을 unseen class로 예측하는 것이다.

 

 그렇다면 어떻게 unseen example을 예측하는 것일까?

이렇게 zero-shot class 문제를 풀 때는 보조적인 속성정보가 필요하다.

보조적인 속성정보가 될 수 있는 후보들과 예시는 다음과 같다.

• Attribute : 동물 종류에 대해 예측할 경우 부리, 발톱 등 구조화된 속성 정보
• Text : wikipedia corpus로 구축된 embedding
• Class Similarity : data class embedding 간 유사도

 이러한 보조 정보는 semantic embedding vector로서 training example을 통해 학습된다. 이를 바탕으로 unseen class에 대해서도 semantic 정보로 그 class를 예측할 수 있는 것이다.

 

 이는 인간이 과거의 경험적 지식 또는 의미 관계를 바탕으로 새로운 것을 유추해내는 능력에서 비롯된 방법론이다. 아이에게 얼룩말과 사슴의 사진을 보여주고 두 동물의 특징이 모두 있는 동물을 오카피라고 하면 아이가 오카피의 사진을 추론할 수 있는 그 원리이다. 

 

 다시 정리하자면 zero-shot learning은 특정 문제에 대해 학습한 경험이 없어도 이미 저장된 데이터를 변형하고 해석하여 학습했던 문제와 학습하지 않았던 문제 간의 특징을 분석하여 답을 예측하는 것이다.

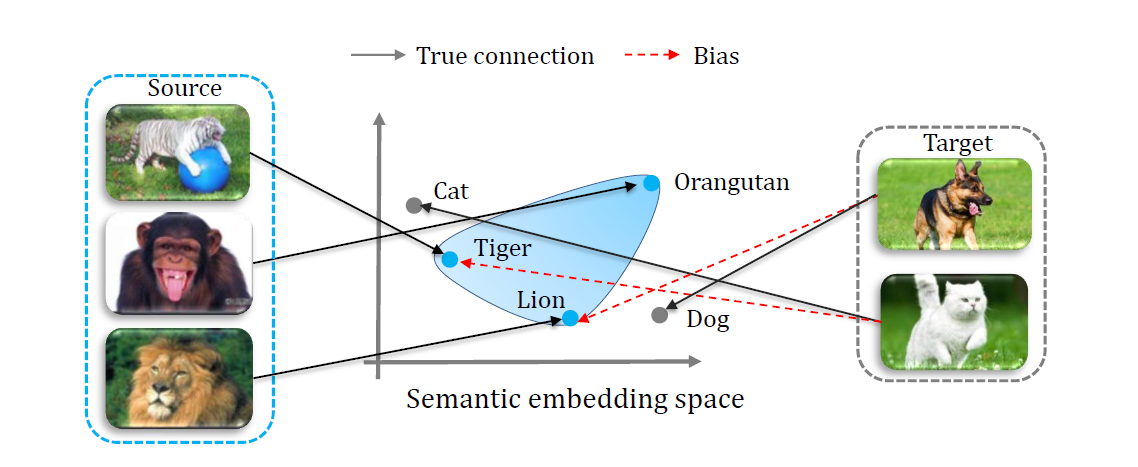
2) Main Idea of Paper

 

  이 논문의 main idea는 다음과 같다.

 

• Goal : 자연어 knowledge를 사용하여 unseen class 이미지를 예측
• Idea
  • 이미지를 nn 모델로 학습된 단어의 의미적 공간에 매핑
     : Large, unsupervised text corpus로 생성된 word embedding space에 이미지가 매핑되면서 word vector는 함축적으로 visual modality를 기저로 하게 됨
    
    >> unseen class에 대한 accuracy를 높임
    
    
  • 모델은 새로 입력되는 이미지가 seen class인지, unseen class인지 판단하는 novelty detection을 가짐 
    : 앞서 말했듯, classifier는 test 이미지를 seen training example class로 분류하는 것을 선호하기 때문
    
    >> seen class에 대한 높은 accuracy를 유지

---

2. Related Work

 

1) N-Shot Learning

 

 여기서의 N은 training에 활용되는 class별 example의 갯수이다. 이 N에 따라 학습 방식은 아래와 같이 구분된다.

• Zero-Shot Learning : training 시 사용되는 example 수가 0개 = unseen class를 test 시에만 확인 가능 
• One-Shot Learning : training 시 사용되는 example 수가 1개
• Few-Shot Learning : training 시 사용되는 example 수가 매우 적은 경우

 학습 방식에 따라 N-way K-shot 문제로 명명되는데 이 때 N = 범주의 수 / K = class별 서포트 데이터의 수 이다.

아래의 예시는 2-way 5-shot 문제이다.

 

 

 

 2) Multimodal Embedding

 

 Multimodal Learning 이란 인간의 5가지 감각기관으로 수집되는 다양한 형태(modality)의 데이터를 사용하여 모델을 학습하는 것을 말한다. 

 

 Multimodal은 이 감각의 종류가 많다는 것이 아니라 이 감각들이 다른, 즉 차원 자체가 다른 변수들로 구성되어 있다는 것이다. 여기서 이런 다양한 감각들의 연관된 데이터는 같은 공간에 비슷한 위치로 매핑하는 multimodal embedding이다.

 

---

3. Methodology

1) Word and Image Representation

 

  이 논문의 제목과 같이 여기서의 cross-modal은 단어와 이미지 간의 매핑의 경우이다. 각각 어떻게 표현되는지 살펴보자.

 

• Word Representation
  • 단어는 distributed vector로 변환되고 context 내의 단어에 대해 co-occurence를 기반으로 표현된다. 여기서의 distributional approach는 단어들 간에 의미적 유사성을 확인하기 위해 자주 쓰이는 방식이며 distributed vector로 표현하는 방식은 nlp 분야에서 효과적인 방법이다.
    
    
  • word vector는 50차원의 pre-trained된 vector로 initialize되며 이 모델은 위키피디아 text를 이용해 각 단어가 context에서 발생할 가능성을 예측하여 학습된 결과물이다.
    
    
  • 이 모델은 local context와 global document context를 모두 이용하여 semantic(통사적), syntatic(의미적) 정보의 분포를 모두 잘 포착하게 된다.

 

• Image Representation
  
  • Cost et al 이 제안한 unsupervise 방식을 통해 이미지 I개의 feature를 추출
  • image representation vector는 I 차원을 가지게 된다.

2) Projecting Images into Semantic Word Spaces

 

 

 

 이미지와 단어 간의 매핑을 훈련시킬 때 사용하는 목적함수는 위와 같다. 이 목적함수를 최소화하는 방향은 nn이 학습되고 짝을 이루는 이미지와 단어의 embedding 위치가 거의 동일하도록 학습된다.

 

 논문에서는 two-layer nn이 single linear mapping보다 더 좋은 성능을 낸다고 밝혔다.

 

 다음 그림은 word vector와 image로 seen class와 unseen class의 semantic space를 시각화한 것이다. 이 때 t-SNE를 통해 50차원인 semantic space를 2차원으로 축소하여 시각화하였다.

 

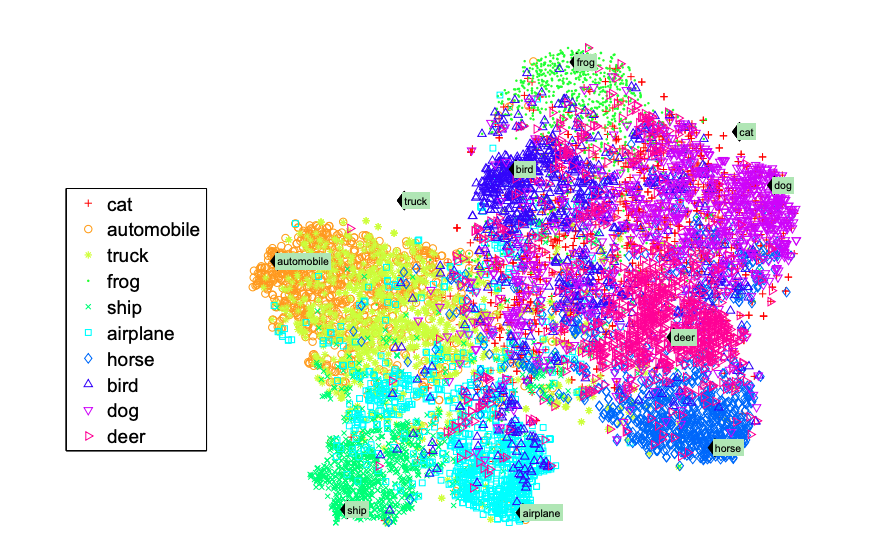
 위 시각화 결과에서 알 수 있듯이, 대부분의 class는 각 대응되는 word vector들끼리 군집을 이루고 있는 것을 확인할 수 있다.

하지만 unseen class인 cat이나 truck의 경우 군집들과 떨어져 있다. 이 때 truck은 automobile, cat은 dog의 군집과 가까이 위치해 있는데 위 목적함수와 학습방식의 결과로 의미적으로 유사한 벡터와 가깝게 위치하고 있음을 알 수 있다.

 

  이러한 방식으로 unseen class 이미지를 detection하고 이를 zero-shot word vector라고 분류할 수 있다.

 

 

3) Zero-Shot Learning Model

 

  다시 말하자면 이번 model의 목표는 테스스텟의 이미지 x에 대한 조건부 확률 P(y|x)를 예측하는 것이다. 이 때 y는 seen, unseen class를 모두 포함하고 있다.

 

 그리고 일반적인 classifier는 training example에 없었던 class를 예측할 수 없기 때문에 binary novelty random variable V를 사용하여 어떤 image가 seen, unseen class인지를 먼저 예측하게 된다.

 

 새로운 input image x와 그 semantic vector f 를 바탕으로 class y를 예측하는 태스크는 다음의 수식으로 P(y|x)를 구해 이뤄진다.

 

 

 

 

4) Novelty Detection

 

 앞서 언급했듯 해당 논문에서는 unseen class 구분을 위한 novelty detection 방식을 사용하는데 위 수식 기준 marginalized term에서 V=u일 경우의 확률이 입력된 이미지가 unseen class일 확률이다.

 

 아래 그림과 같이 unseen class는 training 이미지들과 아주 밀접하게 위치하진 않지만 대략적으로 같은 semantic region에 위치해 있는 것을 볼 수 있다. 이러한 특징을 기반으로 outlier detection 방식을 seen과 unseen class 구분에 활용할 수 있는 것이다.

 

 

 

 outlier detection에 사용할 수 있는 방법론은 다음과 같이 두가지가 있다.

 

• 간단한 threshold 활용

(1) isometric한 class-specific 가우시안 분포 하에서 각 이미지에 대한 marginal를 부여. 이 때 seen class의 mapped point로 이 marginal를 구함.

(2) 각 seen class y에 대해 다음을 연산각 class의 가우시안 분포는 해당 label을 가진 모든 training point로 추정된 word vector wy를 평균으로, sigma y를 공분산으로 가짐

 

 

(3) 새로운 이미지 x에 대해 다음의 indicator function으로 outlier가 detection 됨

 

   

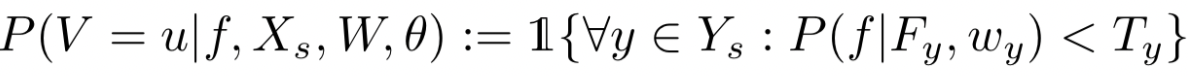
  여기서 threshold Ty보다 주변확률 값이 낮으면 outlier, 즉 unseen class로 분류되고 Ty값이 작을수록 unseen 이미지가 적어진다.

 

 하지만 이렇게 threshold를 사용하는 방식은 outlier에 대해 실제 확률값으로 설명하지 못한다는 단점이 있다.

---

• LoOP (local outlier probabilities)를 이용

(1) unsupervised 방식으로 실제 outlier 확률값을 얻은 후, seen class와 unseen class classifier를 가중 결합하여 조건부 확률을 구함. 이 방식대로라면 모든 unseen image가 outlier로 인식되는 것은 아니지만 seen class에 대해 높은 accuracy를 유지할 수 있다.

 

(2) k = outlier인지 결정하는데 사용되는 nearest neighbors의 개수

 

(3) lambda = 표준편차의 계수 (값이 클수록 군집의 평균으로부터 어떤 지점이 더 멀리 떨어져 있음을 의미)

 

(4)  각 unseen class test 이미지의 semantic vector인 f에 대해 seen class의 training set 안에서 k nearest neighbors의 context set C(f)를 정의하고 probabilistic set distance(pdist)를 계산

 

 

여기서의 d(f,q)는 word space상의 distance function을 의미하고 유클리디언 거리로 계산했다.

 

(5) local outlier factor(lof)를 다음과 같이 정의해 큰 lof 값은 outlier가 증가함을 의미한다.

 

 

(6) threshold outlier detection 방식과 다르게 실제 outlier에 대한 확률값을 구하기 위해 normalization factor Z를 정의하고 이는 seen class의 train set에서의 lof(q) 값에 대한  표준편차이다.

 

 

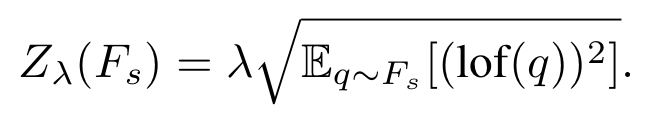
(7) lof와 Z을 통해 local outlier probability를 아래처럼  구한다.  이렇게 구한 LoOP값으로 새로운 test 이미지에 대한 outlier 정도를 기반으로 seen과 unseen classifier를 검토하는데 사용된다.

 

5) Classifier

 seen class와 unseen class 각각의 그룹끼리 별도의 classifier를 적용한다.

 

 

• seen class (V=s) : 어떤 classifier를 써도 상관없으며 논문에서는 sofmax classifier를 사용한다.
• unseen class (V=u, zero-shot) : unseen class word vector의 분포를 isometric Gaussian distribution으로 가정하여 likelihood를 바탕으로 class label을 부여한다.

---

4. Experiment

 

1) Setting

• 데이터셋 : CIFAR-10
• 이미지 : unsupervised feature extraction 방식(Coates & Ng)으로 12,800 차원의 feature vector를 추출
• 단어 : Huang dataset으로부터 50차원의 vector를 사용하고 CIFAR10의 class와 매핑 가능한 대상
• CIFAR-10 10개의 class 중 8개의 class를 training에 사용하고 남은 2개 class는 zero-shot exmaple로 사용

 

2) Result

• Seen & Unseen classes Seperately
  • softmax classifier로 8개 class에 대해 학습 >> accuracy 82.5% 
  • 2개의 unseen class(zero shot class)에 대한 classification = isometric Gaussian 사용
    • (dog - cat) 이 함께 2개의 class로 빠지게 되면 dog은 8개 중에 cat이 없어, cat은 8개 중에 dog이 없어 분류가 제대로 되지 않음. (남은 8개 중에서 dog, cat과 유사한 것이 없어 좋은 semantic 정보를 활용할 수 없음)
    • (cat-truck) 이 빠질 경우 8개 중 dog와 car이 있어 zero-shot 성능이 좋았음 >> max accuracy 90%

 

• Influence of Novelty Detectors on average accuracy
  • seen/unseen class에 대해 novelty detection을 거친 후 class를 예측했을 때의 accuracy를 분석한 결과,
    • Gaussinal model은 unseen class로 예측하는데 덜 보수적인 모델이기에 unseen fraction이 증가해도 비교적 잘 분류하고 있음 = unseen class에 대한 accuracy가 급격히 감소하지 않음
      
      
    • LoOP model은 unseen class로 분류하는데 보수적이어서 대부분의 이미지를 seen으로 분류하여 fraction이 증가하면 unseen에 대한 accuracy가 줄어듦
      
      
      • 따라서 seen과 unseen 중 어느 class 분류의 accuracy에 집중할지에 따라 threshold를 조절하고 classifier를 선택해야 한다!

 

• Combining predictions for seen and unseen classes
  • 방법론에서 의도 했던대로
    • LoOP 모델은 outlier에 대한 probability 값을 그대로 사용
    • Gaussian 모델은 threshod를 설정해 log probability로 변환하여 사용
      
      
• Importance of Feature Mapping
  • 고안한 방법론인 novelty detection 이전에 image feature를 word space 상에 매핑하는 것이었음.
  • 그렇다면 이 매핑 작업없이 Gaussian model을 원래의 image feature에 적용한다면?
    • word space 상에서 outlier로 예측한 100개의 이미지 :  false positive rate = 12%
    • original image feature space 상에서 예측한 100개의 이미지 : false positive rate = 78%
      • original space 상에서는 이미지들끼리 스스로 gaussian centroid를 추론해야 하는데 이 결과물은 각 class의 center를 대표하기 어려움
• Extenstion to CIFAR-100(4개 class는 word vector가 존재하지 않아 제거하고 CIFAR-10을 합쳐 총 106개 class로 진행)
  • 6개를 zero-shot class로 분리
    • seen class >> accuracy = 52.7% (baseline과 유사)
    • unseen class >> accuracy = 52.7% 
    • 이미지를 word space로 매핑할 때 nn의 layer 갯수가 1개일 때 보다 2개일 때 성능이 더 좋음
      
      

 

• Zero-Shot classes with Distractor Words
  • 많은 수의 unseen classes 중에서 zero-shot 이미지를 잘 분류하는지 확인
  • 실험 세팅 추가 = distractor words 추가
    • 1번 : 무작위로 random noun을 semantic space에 추가
    • 2번 : k개의 이웃하는 word vector를 추가 (cat에 대해 kitten 추가)
  • 1번의 경우 성능 저하가 거의 없음 >> 이미지의 word space 매핑이 잘 이루어지고 있음
  • 2번의 경우 성능이 저하되다가 수렴함 >> 유사한 unseen category에 대해서는 정확한 분류가 어려움