고정 헤더 영역
상세 컨텐츠
본문 제목
[Dive into Deep Learning / 2주차] PyTorch Automatic Differentiation
본문
작성자 : 16기 하예은
본 포스팅은 다음 자료들을 참고하여 작성되었습니다.
- https://d2l.ai/chapter_preliminaries/autograd.html
- Mathematics for Machine Learning(Marc Peter Deisenroth, A. Aldo Faisal, and Cheng Soon Ong)
- https://youtu.be/QFP2Y28dPjM
1. Automatic Differentiation (자동 미분) 이란?
- 정의
- 자동미분이란 컴퓨터 프로그램에서 지정한 함수의 도함수를 평가하는 일련의 기술을 말한다. - 배경
- 인공신경망에서 최적의 파라미터를 찾으려면 모델의 손실함수가 최소가 되는 지점을 찾아야 한다. 이를 위해서는 손실함수에 대한 미분이 진행되어야 하는데, 수작업으로 일일히 미분을 하기에는 시간 및 비용이 소모될 뿐만 아니라 에러가 날 확률이 높다. 따라서 PyTorch에서는 자동으로 미분을 계산해주는 Automatic Differentiation 기능을 제공한다. - 원리
- chain rule을 적용하여 단계적으로 미분한다.
2. Chain Rule (연쇄 법칙)

x에 대한 함수 f, g가 합성된 아주 단순한 상태를 가정해보자.
이 합성함수에 대한 미분은 (g를 f에 대해서 미분한 값) * (f를 x에 대해서 미분한 값)이 된다.
이제는 f가 x1과 x2에 대한 함수이고, x1과 x2는 각각 t에 대한 함수라 하자.
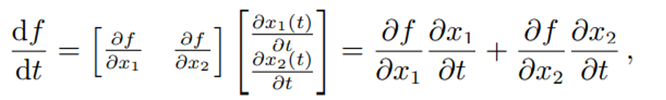
f를 t에 대해 미분을 한다고 하면, f를 x1에 대해 미분한 값과 x2에 대해 미분한 값에 대한 행렬과, x1을 t에 대해 미분한 값과 x2를 t에 대해 미분한 값에 대한 행렬 간의 곱으로 표현된다. 따라서 위과 같은 식의 합으로 표현할 수 있는 것이다.
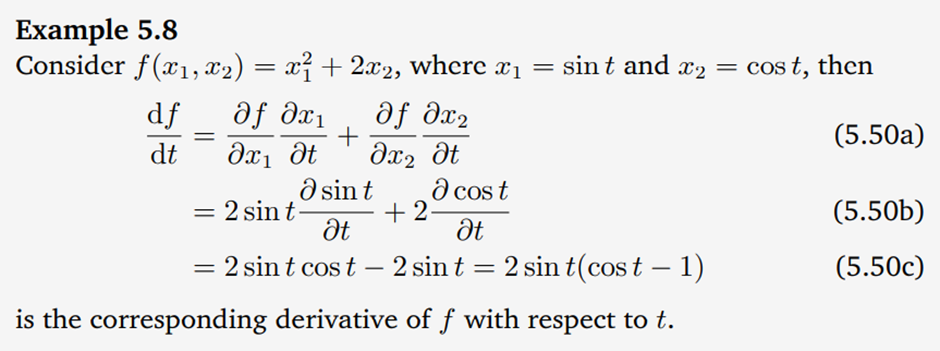
f를 x1에 대해 미분한 값은 2*x1이므로 2*sin(t)가 되고, f를 x2에 대해 미분한 값은 2가 된다.
x1을 t에 대해 미분하면 cos(t)가 되고, x2를 t에 대해 미분하면 -sin(t)가 된다.
따라서 f를 t에 대해 미분한 값은 2*sin(t)*(cos(t)-1)이 되는 것이다.
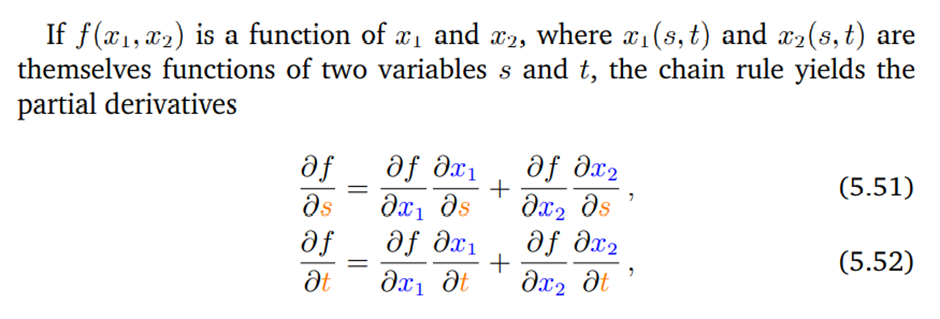
만약 x1과 x2가 s와 t에 대한 식이라고 하면 s와 t에 대한 각각의 미분 값은 위와 같이 표현될 수 있다.
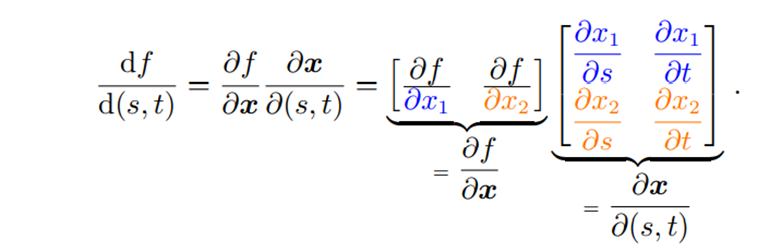
f를 s와 t 모두에 대해 미분하고 싶다면 미분 값은 위와 같다.
3. Chain Rule in Automatic Differentitation
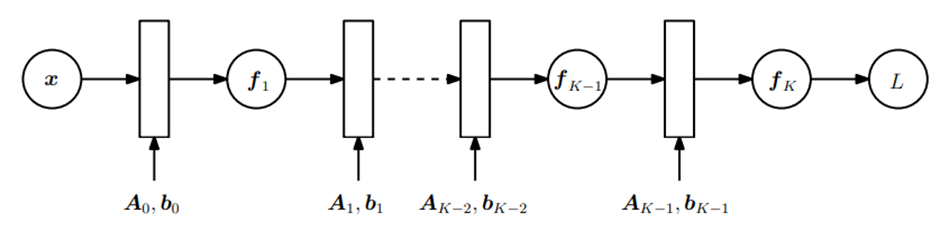
인공신경망은 위의 그림과 같이 여러 개의 층으로 구성 되어있고, 각각의 층은 다음과 같은 식으로 표현된다.

이러한 식 f에 대해서 우리의 손실 함수는 아래와 같이 표현할 수 있다.

이 손실함수가 최소가 되는 값을 찾기 위해서 손실함수에 대한 미분이 필요하다. 여기서 chain rule이 적용된다.
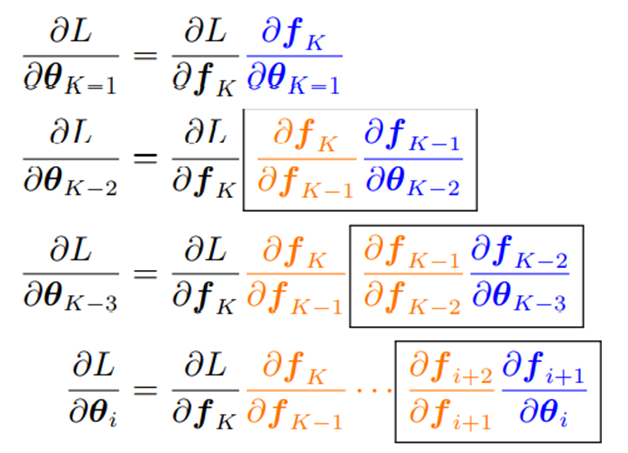
궁극적으로 손실함수 L을 세타 i에 대해 미분한 값은 chain rule을 통해 위와 같이 표현될 수 있다.
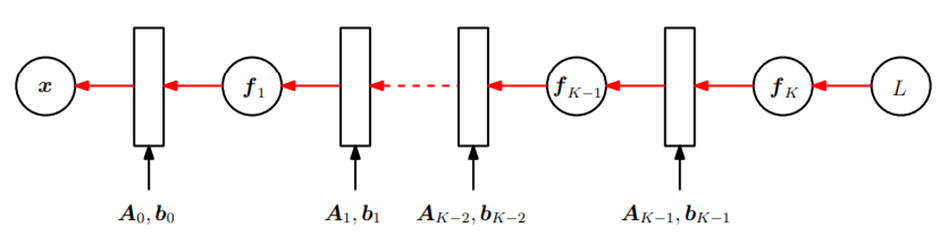
chain rule을 통해 미분하는 흐름을 살펴보면, 마지막 함수인 L에 대해서 f(k), f(k-1), … f(1), x의 순으로 역방향으로 진행되기 때문에 이를 backpropagation이라고 한다.
이를 단순화해서 정리해보자. 우리의 input variable인 x가 output variable인 y로 가는 데에 있어 intermediate variable인 a,b를 거친다고 하자. x로 y로 미분하면 chain rule을 적용하여 다음과 같이 표현할 수 있다.

위의 미분 값은 두 가지 방식으로 구할 수 있다. x로 시작해서 y의 방향으로 미분해 나가면 forward mode, y로 시작해서 x의 방향으로 미분해 나가면 reverse mode이다. 여기서 말하는 reverse mode가 앞서 언급했던 back propagation(역전파)와 동일하다.

즉, automatic differentiation은 intermediate variable들을 사용해서 단계적으로 미분을 하는 것이라고 할 수 있다.
4. PyTorch로 구현하기

우리가 y=x^2이라는 식에 대해서 미분을 한다고 해보자. 먼저 x를 0, 1, 2, 3으로 구성되어 있는 텐서로 할당한다.

계산하기 전에 계산 값을 저장할 수 있는 x.grad를 생성해준다.

이제 y를 생성해주면 28이라는 스칼라 값이 계산되어 나오고 x에 대해서 곱하기가 되었다는 내용이 출력된다.

y에 대해서 backward를 해주고 x grad를 살펴보면 grad에는 x에 4가 곱해진 값, 즉 4x에 대한 결과값이 저장되어 있는 것을 확인할 수 있다.
하지만 y가 scalar가 아닐 때에 backward함수를 사용하면 에러가 발생하게 된다. 이에 대한 해결책은 scalar가 아닌 y를 어떻게 scalar로 만들지에 대해서 지정을 해주는 것이다.
5. Backward for Non-Scalar Variables
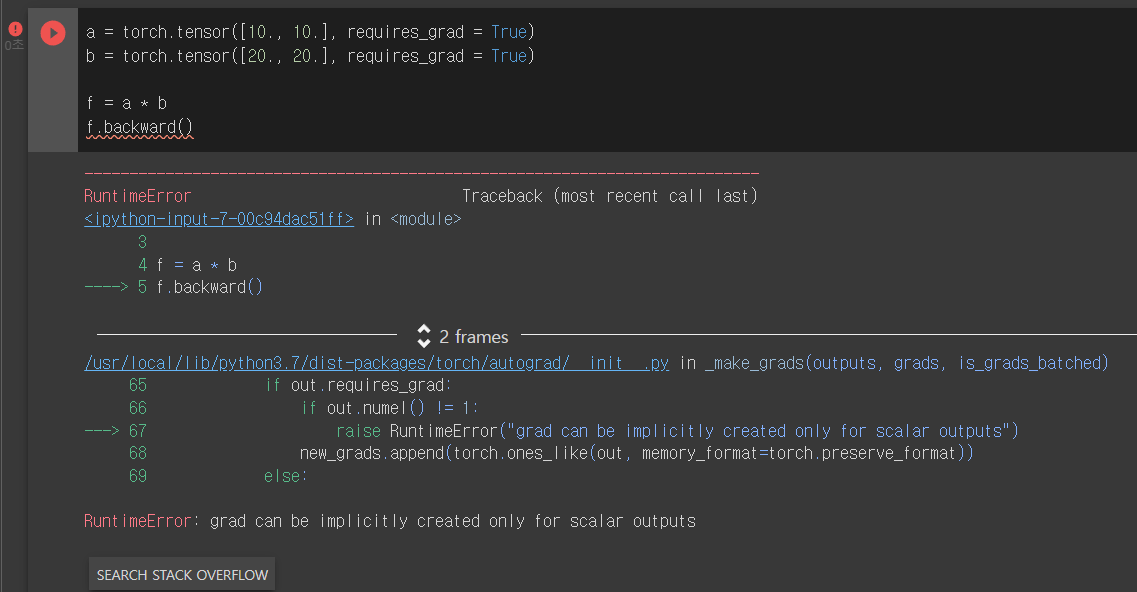
f가 scalar 값이 아닐 때 backward 함수를 사용하였더니 'grad can be implicitly created only for scalar outputs'라는 RuntimeError가 발생하였다.

그러나 gradient = torch.tensor([1., 1.]))을 지정해주었을 때는 에러 없이 a.grad와 b.grad가 출력되는 것을 볼 수 있다.
어떠한 원리로 작동하는 것일까?

gradient는 Jacobian matrix와 vector(v)의 행렬곱으로 계산된다. 여기서 Jacobian matrix는 도함수 행렬이다.
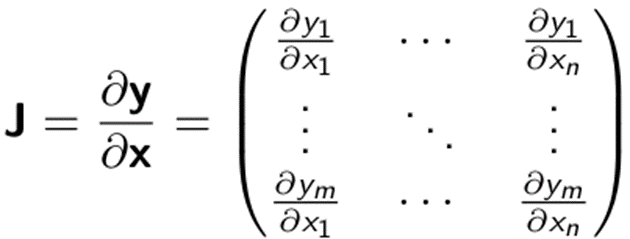
backward함수의 default 값은 backward(gradient = torch.tensor([1.])이기 때문에 output이 scalar인 경우에는 gradient를 따로 지정해줄 필요가 없다. 그러나 non-scalar인 output에 대해서는 동일한 길이의 vector를 gradient로 지정해주면 에러 없이 gradient를 계산할 수 있다.
'심화 스터디 > Dive into Deep Learning' 카테고리의 다른 글
| [Dive into Deep Learning / CNN] Fully connected layer / pooling layer (0) | 2022.11.13 |
|---|---|
| [Dive into Deep Learning / 3주차] Python Class (2) | 2022.09.30 |
| [Dive into Deep Learning / 2주차] Backward Function Problem (0) | 2022.09.25 |
| [Dive into Deep Learning / 2주차] Tensor Manipulation (0) | 2022.09.25 |
| [Dive to Deep Learning/1주차] 딥러닝이란? (What is Deep Learning?) (1) | 2022.09.18 |





댓글 영역