고정 헤더 영역
상세 컨텐츠
본문
본 포스팅은 김성범 교수님의 강의
https://www.youtube.com/watch?v=noFCkN6gXZ4&list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd&index=8
Exponential Smoothing(지수 평활법) 를 참고하여 작성되었습니다.
작성자:15기 고태영
1. 구간 평균법
과거 시점의 일정기간(N)의 (산술)평균으로 다음 시점을 예측

실제 데이터 적용
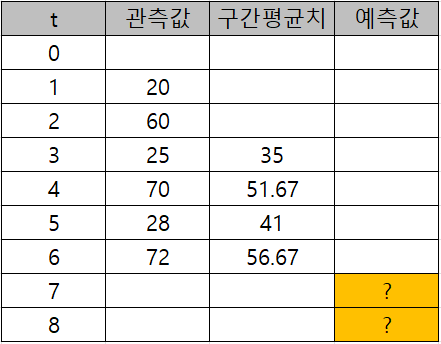
N=3일때, t=6에서의 구간평균치는 어떻게 구할까?
(72+28+70)/3=56.67
구간평균법의 한계
1. 과거 N개의 데이터에 동일한 가중치를 준다
2. 미래의 예측값이 모두 동일하다.
언제 사용하는 것이 좋을까?
특별한 trend, seasonal variation이 없는 데이터, 일정한 크기로 움직이는 데이터
N은 어떻게 결정을 할까?
N이 작을 때: 최근 데이터의 경향을 많이 반영
N이 클 때: 과거 데이터의 경향을 많이 반영
2. 평활법?
=Smoothing
공통점
평균을 취해서 데이터의 노이즈를 편평하게 한다!
한계
spike 패턴이 있는 데이터에 적용하기 어렵다

2-1. 지수평활법
(1)단순 평균이 아닌 가중평균을 이용
(2)지수 분포 모양에 근거한 가중치 결정

처음에는 감소하는 정도가 빠르지만 점점 그 정도가 느려진다.
(3) 모든 과거 데이터를 포함하여 계산
2-1-1 단순지수 평활법

가중치는 0과 1사이의 값, 점점 가중치가 작아진다.
계산 과정

1. 시작점
갖고 있는 데이터(n개)의 평균으로 시작
2. 업데이트
현재 시점의 데이터에는 알파의 가중치, 과거 시점의 데이터에는 (1-알파)의 가중치를 줌.
적용
alpha=0.1
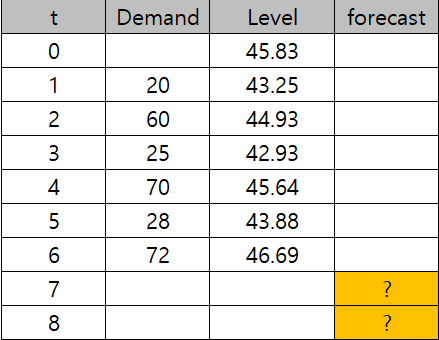
t=0일때의 level: (20+60+25+70+28+72)/6= 45.83
t=1일때의 level: a(20)+(1-a)(45.83)=43.25
t=2일때의 level: a(60)+(1-a)(43.25)=44.93
43.25의 값에는 level0의 값도 누적되어 값음! (과거의 값이 누적된다)=> 앞에서 보았던 (1-a)^n의 효과
한계
모든 미래 시점을 동일한 값으로 예측
a 결정
1)큰 a값 사용-> 최근 데이터에 보다 큰 가중치 적용 ex) 과거의 패턴이 중요하지 않은, 크게 패턴이 없는 smooth한 데이터
2)작은 a값 사용-> 과거 데이터에 보다 큰 가중치 적용 ex)noisy 데이터(과거의 패턴이 예측에 큰 도움을 줄 수 있다)
보편적으로 a=0.2 or a=0.3 => 보통 소프트웨어에서 자동적으로 계산됨
한계
미래시점에 관계없이 예측값 모두 동일-> 트렌드가 있는 데이터, 계절적 변동이 있는 데이터에 적합하지 않음
2-1-2 이중지수 평활법
트렌드가 존재하는 시계열 데이터 예측 시 적합
단순지수평활법을 2번 적용
방법


(1) 단순 선형회귀분석을 이용하여 L_0:절편 ,B_0:기울기 결정
*이때, B_t는 "Growth rate"이며 증가량, 즉 Trend를 나타냄
(2) L값을 Update: 현재시점에 알파만큼의 가중치를 주고, 과거시점에 1-알파만큼의 가중치를 줌
(3) B값을 Update: 현재시점과 전시점의 차이에 베타만큼의 가중치, 지난 시점의 GROWTH RATE에 1-베타 만큼 가중치를 줌
(4) 예측값을 산출할때, B_t의 계수가 증가하며 Trend를 반영할 수 있다
적용
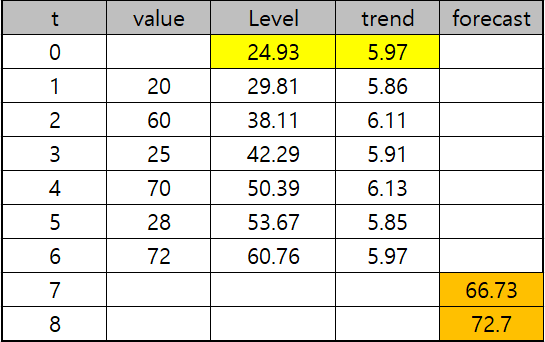
*alpha:0.1, Beta:0.1 가정
t=1일 때, Level_1= alpha(20)=(1-alpha)(24.93+5.97)=29.81
Beta_1= Beta(29.81-24.93)+(1-Beta)(5.97)=5.86
한계
계절적인 변동을 반영하지 못한다.
2-1-3 홀트-윈터 (Holt-Winter) 지수평활법 = 삼중 지수평활법
=> 계절적인 변동을 반영할 수 있다.
종류
(1) Additive Winter's method
계절 변동 산포가 일정할 경우= Constant seaonal variations
(2) Multiplicate Winter's method
계절 변동 산포가 증가할 경우= Increasing seasonal variations

Additive 예측모델

Update!
l_T: Level 상징
b_T:Trend 상징
sn_T: seansonal variation 상징

타워=예측시점
Multiplicative 예측모델


=> 예측값을 구할 때, 계절적 변동을 더해주는 것이 아니라 "곱해줌"

코드 실습
1.시계열 데이터 준비
1991년 7월부터 2008년 6월까지 월 단위(monthly)로 집계된 약 판매량 시계열 데이터셋
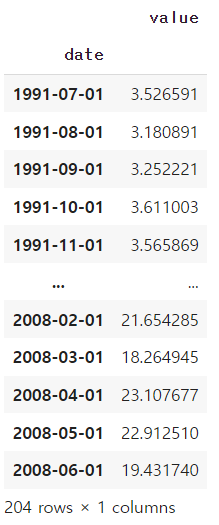
데이터의 형태를 확인해보자...

(a) 선형 추세가 존재합니다. (linear or quadratic trend)
(b) 1년 단위의 계절성이 존재합니다. (seasonality of a year, ie. 12 months)
(c) 분산이 시간의 흐름에 따라 점점 커지고 있습니다. (increasing variation)
2. Train/Test 나누기

Train 데이터

Test data

3. 단순지수 평활법/Additive model/Multiplicative model에 train data를 fit하자!

4. 예측값 확인

5. 모델을 평가해보자

예상대로 Multiplicative model의 성능이 가장 좋다...!!!
'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열 스터디] ARIMA Model part2 (1) | 2022.09.25 |
|---|---|
| [시계열 스터디] ARIMA Model Part 1 (1) | 2022.09.25 |
| [시계열 데이터] Seasonal Variation (0) | 2022.09.23 |
| [시계열 스터디] Time Series Regression (0) | 2022.09.14 |
| [시계열 스터디] 시계열 데이터의 특성 (1) | 2022.09.13 |





댓글 영역