고정 헤더 영역
상세 컨텐츠
본문
* 작성자 : 16기 박종혁
본 포스팅은 고려대학교 산업경영공학부 김성범 교수님 강의를 참고하여 작성되었습니다.
https://www.youtube.com/watch?v=P_3808Xv76Q&list=PLpIPLT0Pf7IqSuMx237SHRdLd5ZA4AQwd&index=10
[ ARIMA 모델 개요 - PART 2 ]
지난 주차 Review
Q1) 정상성의 의미와 확인하는 방법은?
-> 정상성은 시간에 관계없이 평균과 분산이 일정한 성질로 ACF 그래프로 확인
Q2) AR 모델에서 독립변수로 활용되는 것은?
-> 자기 자신의 lag된 데이터(Yt)
Q3) MA 모델에서 독립변수로 활용되는 것은?
-> 각 시점에서의 error(Et)
Q4) AR, MA, ARMA 모델을 사용하기 위해 반드시 만족해야하는 데이터의 특성은?
-> 반드시 정상성을 만족해야 위의 세 가지의 모델 활용 가능
Q5) ARIMA(p,d,q)에서 p,d,q가 각각 의미하는 것은?
-> p : AR 모델에서의 독립변수의 개수
-> d : 차분의 차수
-> q : MA 모델에서의 독립변수의 개수
Box-Jenkins ARIMA procedure
ARIMA Model을 구축함에 있어 사용되는 절차
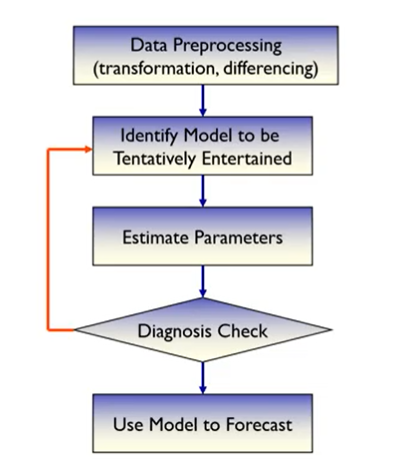
1. Data Preprocessing
- nonstationary data를 stationary data로 변경하기 위하여 데이터 전처리 진행
- Q6) 정상성을 만족시키기 위해 수행하는 대표적인 전처리 방법은? -> 차분(differecning)
2. Identify model to be tentatively entertained
- 임시 모델을 선택
- 이 단계에서 선택한 모델은 최종적인 모델이 아니라 임시 모델이기에 추후 변경 가능
3. Estimate parameters
- 앞선 단계에서 선택한 모델을 바탕으로 모수 추정
4. Diagnosis check
- 해당 모델이 모수를 잘 추정하였는지 확인
- 해당 모델이 적절하지 않다고 판단되면 2단계로 돌아가 새로운 모델 선택
5. Use model to forecast
- 적합한 모델을 찾아 최종적인 모델로 선정
실제 데이터를 활용한 Box-Jenkins ARIMA procedure
1. Raw data plotting

- 원자료의 그래프를 통해 정상성 여부 파악하기
- 대부분의 자료가 위의 그래프만으로 정상성 여부를 명확히 파악하기 쉽지 않음
2. ACF로 보다 정확한 정상성 확인

- ACF 그래프가 급격히 감소하거나 일정한 패턴이 없는 경우 -> stationary
- ACF 그래프가 천천히 감소하는 경우 -> nonstationary
- Q7) lag가 0일 경우 유의미한 정보를 가지지 않는 이유는? -> 자기 자신과의 상관계수는 항상 1이기 때문
3. 차분(differencing) 진행
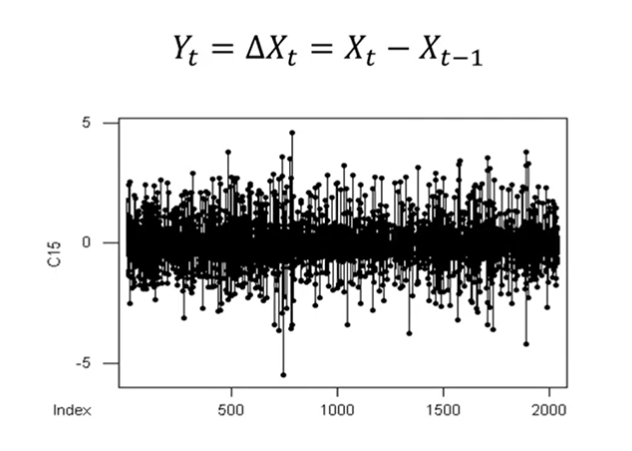
- 이 데이터의 경우 1차 차분 진행(대부분의 경우 1차 차분 진행)
- 정상성이 존재함을 확인 -> 평균 및 분산이 일정

- Q8) 위 그래프를 바탕으로 정상성이 존재함을 알 수 있는 근거는? -> lag가 1인 시점 이후부터 급격히 감소
4. 임시 모델 선정
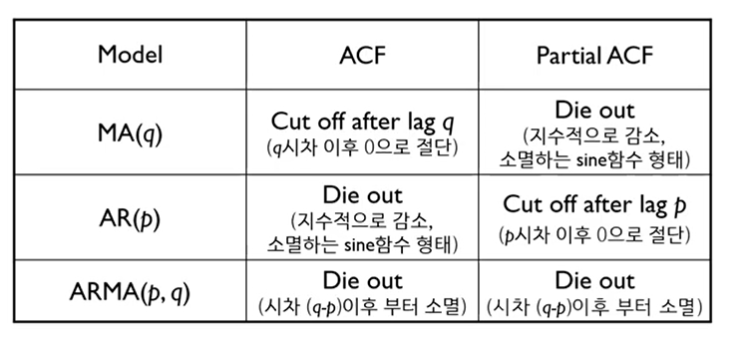
- ACF와 PACF에 대해 보다 상세한 내용을 학습하려면 아래 링크 참고!!
- https://direction-f.tistory.com/65

- (a) lag가 2인 시점 이후부터 급격하게 감소하는 양상
- (b) ACF 그래프가 지수 형태로 감소하는 양상
- (c) ACF 그래프가 sine형태로 감소하는 양상
- (d) ACF 그래프가 진동하면서 감소하는 양상
- (a)의 경우 cut off, (b), (c), (d)의 경우 die out 한다고 볼 수 있음
- ACF와 PACF 그래프를 바탕으로(graphical method) AR, MA, ARMA 모델 중 적합한 것 선정
- 주관적인 해석이 반영된다는 점에서 한계점 존재
- 최근 컴퓨터 기술의 발달로 p,d,q의 가능한 모든 경우의 수에 대해 정확성 비교
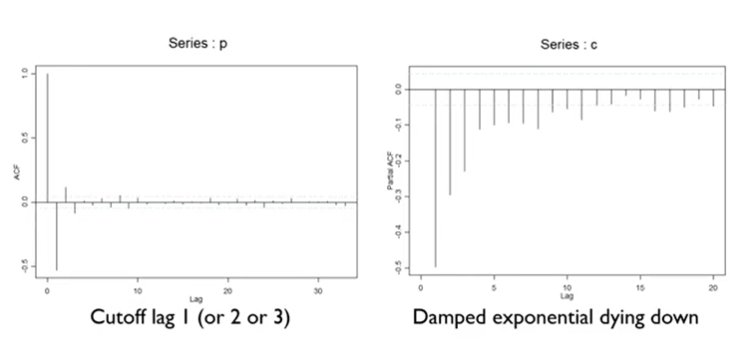
- ACF 그래프의 경우 lag가 1 이후에 급격히 감소하는 형태
- PACF 그래프의 경우 천천히 감소하는 형태(지수적)
- Q9) 따라서 어느 모델을 선정하는 것이 바람직한가? -> MA(1) 모델 선정
5. 모수 추정

- MA(1) 모델을 비롯하여 비슷한 다른 형태의 모델에 대해서도 모수 추정 진행
- 모델 선정 시 대표적으로 사용되는 수치는 AIC
- Q10) AIC를 바탕으로 모델을 선정하는 방법은? -> 보다 더 낮은 AIC를 가지는 모델을 선택

- 비슷한 모델에 대해서 AIC를 구한 결과 ARIMA(0,1,3) 모델이 가장 적합 -> 아직 임시 모델!
6. Diagnosis check
- 잔차에 대한 ACF를 생성한 후 대부분의 residual이 bound 내에 있으면 적합하다고 판단
- 이 때 bound는 평균에서 3*(residual의 표준편차)를 더하고 뺌으로써 설정
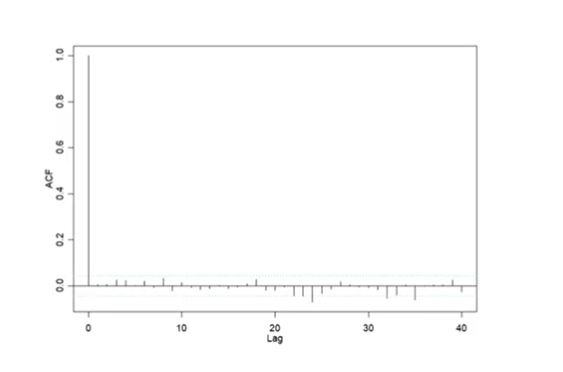
- 대부분의 residual이 bound 내에 있으므로 ARIMA(0,1,3) 모델은 적합하다고 판단
7. Forecasting
- 적합하다고 판단된 모델을 이용하여 새로운 데이터에 대해 예측을 진행
Seasonal ARIMA model (SARIMA)
- 기존 ARIMA 모델에 계절 변동을 반영한 모델
- SARIMA 모형은 각 계절에 따른 독립적인 ARIMA 모델이 합쳐져 있는 모델
- 기존 ARIMA(p,d,q) 모형에 계절성 주기를 나타내는 차수 s가 추가되어 ARIMA(p,d,q)(P,D,Q)s로 표기
- Q11) 월별 계절성을 나타낼 경우와 분기별 계절성을 나타낼 경우 s값은? -> 월별 : 12, 분기별 : 4


'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열] ARIMA 모델 - Part 4 (0) | 2022.11.03 |
|---|---|
| [시계열 스터디] ARIMA Model part3 (0) | 2022.10.09 |
| [시계열 스터디] ARIMA Model Part 1 (1) | 2022.09.25 |
| [시계열 스터디] Exponential Smoothing (0) | 2022.09.25 |
| [시계열 데이터] Seasonal Variation (0) | 2022.09.23 |





댓글 영역