[CV 논문 리뷰 스터디 / 3주차 / 엄기영] Generative Adversarial Nets, 2014

Paper:

Generative Adversarial Networks

---

Abstract

논문에서는 적대적과정(adversarial process)을 통해 generative model(생성모델)을 추정하는 새로운 방식을 제시한다.

생성 모델인 G는 데이터의 분포를 알아내고, discriminative model(분별모델) D는 생성된 샘플이 G가 아닌 training data에서부터 나왔을 확률을 추정한다.

G의 학습에서는 D가 실수를 할 확률을 최대화 하는 과정으로 이루어진다. 논문에서는 이러한 과정을 minimax two-player game이라고 표현한다.

 

임의의 함수 G와 D의 공간에서는 하나의 "정답"이 존재한다. :

 

G는 training data의 분포를 최대한 복원하는 것이고,

D는 1/2이 되는 것이다(G가 생성한 데이터 분포와 실제 데이터 분포를 구별하지 못한다는 의미).

 

G와 D가 다중 레이어 퍼셉트론들로 구성된 경우 전체 시스템은 backpropagation(역전파)으로 학습이 가능하다. 마코브 체인이나, unrolled approximate inference network등은 학습이나 생성과정에서 필요되지 않는다. 논문에서는 실험을 통해 이렇게 생성된 샘플들에 대한 질적, 양적인 평가를 통해 이 프레임워크의 잠재성을 입증했다.

Introduction

딥러닝은, 이미지, 언어가 포함된 오디오 데이터, 혹은 자연어 말뭉치의 기호들의 확률 분포를 풍부하게 잘 설명하는 모델을 발명하는 것이라고 할 수 있다. 현재까지는 discriminative(분별)모델에서 가장 큰 성공을 얻을 수 있었고, 이는 주로 고차원의 풍부한 sensory 정보를 class 라벨로 매핑시키는 모델이었다. 이러한 성공은 잘 작동하는 gradient를 갖는 piecewise linear unit을 사용하는 역전파 알고리즘이나, dropout으로부터 기반되었다.

 

심층 생성 모델은 최대우도 추정법(maximum likelihood estimation)과 같은 매우 다루기 어려운 확률 연산을 approximate하기 어렵다는 점과, generative(생성) context에서 piecewise linear model을 활용하기 어렵다는 점 때문에, 앞서 얘기한 성공의 영향이 적었다. 이에 논문에서는 이런 단점을 해결할 수 있는 새로운 생성모델 추정 방법에 대해 제안한다.

 

제안된 adversarial(적대적) nets 프레임워크에서 생성 모델은 판별(샘플이 생성 모델 분포에서 나온 것인지, 혹은 실제 데이터 분포에서 나온 것인지 결정하는 방법을 학습)모델과 적대적인 관계를 이루게 된다.

 

마치 생성 모델은 위조 화폐를 만드는 위조범, 그리고 판별 모델은 이를 탐지하려는 경찰처럼 작동을 하게 된다.

 

이러한 두 모델의 경쟁은 위조품과 진품이 구별 불가능할 때 까지 생성모델의 성능을 개선하도록 만든다.

 

이 프레임워크는 다양한 모델과, 최적화 알고리즘들에 적용될 수 있는 특정한 학습 알고리즘을 생성할 수 있다. 논문에서의 경우, 생성 모델은 multilayer 퍼셉트론에 random noise를 전달하는 방법으로 샘플을 생성하고, 판별모델 또한 multilayer 퍼셉트론으로 되어있는 특수한 경우에 먼저 가정을 두고 있다. 

 

이러한 특별한 경우를 논문에서는 적대적 네트워크(adversarial nets)라고 칭하며, 이러한 경우에 두 모델을 성공적인 역전파 과정과 dropout 알고리즘만으로 학습시킬 수 있고, 생성 모델의 forward propagation으로 샘플을 생성할 수 있다. 이 과정에는 approximate inference나 마코프체인 등이 필요하지 않다.

 

Adversarial Nets

먼저 notation들에 대해 정리를 하는 것이 이해에 용이할 것 같아, 논문 내용 이전에 이에 대해 먼저 설명해보겠다.

 

• px : 데이터들에 대한 확률 분포로, 실제 데이터와 생성된 데이터를 포함.
• pdata : 실제 데이터의 확률 분포
• pg : 생성모델이 추정한 데이터 x에 대한 확률 분포
• pz : input noise의 확률 분포
• x : 판별에 사용되는 데이터
• z : 노이즈 데이터
• G(z; θg) : z를 이용한 생성 모델의 매핑 z = G(x), 생성자
• G : 미분 가능한 함수이자, 파라미터가 θg 인 멀티레이어 퍼셉트론
• D(x; θd) : x를 이용한 판별 모델의 매핑 D(x) = p(x가 pg에서 나오지 않음) = p(x가 pdata에서 나옴), 판별자

 

Adversarial modeling framework는 두 모델이 모두 multilayer 퍼셉트론 일 때 가장 간단히 적용할 수 있다. 데이터 x에 대한 생성자의 분포 pg를 학습하기 위해, input noise 변수인 pz(z)를 먼저 정의한다.

 

그런 뒤 데이터 공간(x region)으로의 매핑(샘플 생성 후 데이터 공간으로 이동)을 G(z; θg)로 표현한다. G는 미분 가능한 함수로, 파라미터가 θg인 multilayer 퍼셉트론이다.

 

두 번째 멀티레이어 퍼셉트론의 경우 D(x; θd)로 정의되며 output으로는 하나의 상수값을 낸다. D(x)는  x가 pg가 아닌 데이터로 부터 왔을 확률을 의미하며, training example과 G로부터 생성된 샘플에 대해 정확한 라벨을 달 확률을 최대화 하도록 학습되며, 동시에 G는 log(1-D(G(z)))를 최소화 하도록 학습된다.

 

이를 정리하면 D와 G가 아래와 같이 Value function이 V(G, D)인 two-player minimax game을 진행한다고 생각할 수 있다.

 

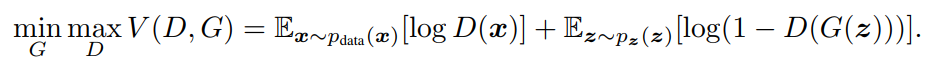
이 수식을 조금 자세히 살펴보자, 먼저 판별 모델인 D의 경우, 어떤 샘플이 주어졌을 때, 이 샘플이 데이터로부터 온건지, 아니면 생성모델 G가 만들어낸 샘플인지를 구별하며, 실제 데이터로부터 왔을 확률을 output으로 낸다. 즉 D가 1에 가까운 수를 output으로 낼 수록 확인한 샘플이 실제 데이터로 부터 왔을 확률이 높다는 것이고, 반대로 0에 가까울 수록 생성모델로 부터 나온 샘플일 확률이 높다.

 

두 번째로 G(z)의 경우, input noise z가 주어졌을 때, 적절한 pg를 학습한 뒤 실제 데이터와 유사한 샘플을 생성할 수록(pg가 pdata에 가까워질 수록) D(G(z))의 값은 1에 가까워지고 [log(1-D(G(z)))]는 작아진다, G가 학습이 잘 이루어지지 않은 경우에는 0에 가까워져서 [log(1-D(G(z)))]는 커지게 된다.

로그함수

결국 D는 Value function을 최대화 시키기 위해 pdata로부터 나온 x는 모두 D(x)  = 1이 되게 하고, pz(z)를 x로 매핑한 D(G(z))는 0이되게 만들어야 한다(잘 판별해야 한다), G는 Value function을 minimize하기 위해 최대한 실제값과 가까운 G(z)를 생성하여, D(G(z))에서 더 작은 값을 갖도록 만들어야한다. 이는 pg를 pdata에 수렴하게 만들어야 한다고 해석할 수 있다.

 

조금 더 이해를 쉽게 하기 위해 아래 그림을 살펴보자.

먼저 각각의 선들이 무엇을 의미하는지를 확인해 보면 아래와 같다.

 

• 검정색 점선 : 실제 데이터가 가지고 있는 확률 분포 pdata를 의미한다.
• 파란색 dash(-----)선 :  판별모델로부터 생성되는 확률값 D(x). (px를 pg로부터 구별하는 과정에서 얻어짐)
• 초록색 실선 : 생성모델에서 학습한 확률 분포 pg
• 위쪽 수평선 : 데이터 x의 일부 영역
• 아래쪽 수평선 : input noise z가 샘플된 영역(이 경우에서는 z가 uniform 분포에서 샘플링 되었다.)
• 화살표 : x=G(z) 매핑 과정, 즉 분포 pg를 부과하는 방식을 보여줌
• 학습이 진행되면서 각 분포는 (a) -> (b)로 점점 update된다.

(a) 두 적대적 신경망 D, G가 수렴에 이르기 직전인 상태이다. : pg는 pdata와 유사하고, D는 부분적으로 정확한 상태.

(b) 알고리즘 D가 데이터를 분별할 수 있게끔 학습된 중간 루프 상태, D*(x) = pdata(x)/pdata(x)+pg(x)

(c) G를 업데이트하게 되면서 D에서 얻어진 gradient가 G(z)의 영역을 더 실제 데이터로 분류하도록 유도한 상태

(d) (a) -> (b) -> (c)를 여러단계 거치면, G와 D가 pg = pdata가 되어 더이상 학습이 불가능한 상태에 이르게 됨. 이 상태에서 판별 모델 두 분포의 차이를 구분할 수 없게된다. (D(x) = 1/2)

 

 

Theoretical Results

논문에서는 두 개의 수학적 증명을 통해 지금까지 설명해온 Adversarial modeling framework가 어떻게 원하는 결과를 얻을 수 있는지 설명한다.

 

1 . Global Optimality of pg = pdata

첫 번째로, 왜 pg = pdata 에서 전역 최적해가 되는지 살펴보자.

 

Proposition 1. 어떠한 G가 주어지든 D(x)는 아래와 같은 최적해를 가진다.

Proof. 학습과정에서 D가 최적해를 가지려면 아래와 같은 value 함수 V를 최대화 시켜야 한다. 여기서 E는 기댓값 즉 expectation을 의미하는데, 연속확률변수 x에 대한 기댓값은 그에 대한 확률을 곱하여 적분하는 것으로 구해질 수 있다.

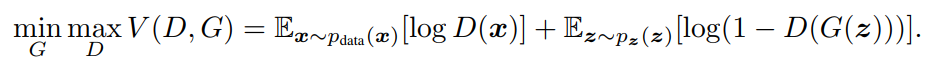
따라서 위 식이 아래의 식으로 변형되고, G는 주어졌으므로(고정), pz(z) -> x = G(z)로의 매핑이 일어나며, 매핑 된 x는 pg의 분포를 따르므로 최종적으로 아래 두 번째 식과 같은 형태로 변환된다. 

0보다 큰 모든 2차원 실수 (a, b) 에서, 함수 a x log(y) + b x log(1-y), y = [0 ,1]는 a/a+b에서 최댓값을 갖는다. 즉 두번째 식의 최댓값은 proposition1이 되고, Discriminator는 *Supp(pdata) U Supp(pg) 외부에서 정의될 필요가 없으므로, Proposition 1의 증명이 완료된다.

 

*위상수학적 표기이나, 플로우상, pdata분포와 pg분포의 외부에서 정의될 필요가 없으니, 주어진 x에 대해 D(x)가 [0 , 1]내의 값을 가진다고 해석해야 할 듯 하다.

 

D를 학습하는 목적은 log-likelihood 를 최대하거나, 조건부 확률 P(Y=y | x)를 추정하는 것이라고 해석 될 수 있다. 여기서 Y는 x가 pdata(y=1)에서 왔는지 혹은 pg(y=0)에서 왔는지를 의미한다. 이에 위의 equation은 다음과 같이 변형시켜 사용할 수 있다.

Theorem 1. Criterion C(G)는 pg = pdata 일 때만 전역 최솟값을 가지며 이 때, C(G)는 -log4의 결과값을 가진다.

proof. pg = pdata 인 경우, D*G(x) = 1/2를 가지게 된다. (Proposition 1에서 대입하면 확인할 수 있다.) 따라서 D*G(x) = 1/2를 위의 equation에 대입하게 되면, C(G) = log1/2 + log1/2 = -log4가 된다. 

 

어떻게 -log4가, pg = pdata 에서 C(G)의 가능한 최적의 값이 되는지 증명할 수 있을까?

 

증명 아이디어 : 방금 pg=pdata로 얻은 결과 값보다 C(G)가 무조건 크거나 같다는 것을 증명하면, -log4가 전역 최솟값임을 증명하게 되는 것과 같다. 

먼저 C(G) = V(D*G, G)에서 빼주게 되면 아래 첫 번째 식을 얻을 수 있다. Expectation연산을 취했기 때문에 각각의 확률과 변수의 값을 곱하고 적분을 취해준 뒤, -log4 값을 log2씩 내부에 더해준다.(어차피 expectation 취하면 상수가 적분 안에서 나와도 같은 값이 되기 때문). 그런 뒤 식을 정리하면 아래 마지막 식과 같은 형태로 변환이 가능하다.

여기서 *KL(Kullback-Leibler divergence)를 이용하면 적분 내의 값들을 아래와 같이 변경할 수 있다.

KL (Kullback-Leibler divergence)
쿨백-라이블러 발산은 데이터가 따르는 실제 확률 분포 P(x)와 모델이 나타내는 확률 분포 Q(x)가 존재할 때, 두 확률 분포의 KL divergence는 두 확률 분포의 차이 즉 P(x)를 기준으로 계산된 Q(x)의 평균 정보량과, P(x)를 기준으로 계산된 P(x)의 정보량의 차이로 정의할 수 있다. 

KL(P||Q)는 위와 같은 형태로 정의되며, 식의 가장 오른쪽 부분을 보면 이는 P(x)를 기준으로 계산한 Q(x)의 교차 엔트로피(Cross entropy)라고도 할 수 있다. 여기서 P(x)의 경우 고정된 값이므로 이러한 쿨백 라이블러 발산을 최소화하기 위해서는 Q(x)가 P(x)와 같을 때, 0이되어 최솟값을 가지고, KL(P||Q)는 0보다 작은 값을 가지지 못한다.

논문에서는 두 KL 식을 Jenson-Shanon divergence 형태로 변환하는데, 일반적인 수식은 아래와 같다.

 

이를 이용해 현재까지 얻어낸 C(G)의 식에 대입하게 되면 아래와 같은 최종적인 형태의 식이 나오게 된다.

이 식을 처음에 C(G)에서 -log(4)를 빼줬던 형태로 다시 변환하면 아래 수식과 같이 변환 될 수 있고, 두 분포(pdata, pg)에 대한 Jenson-Shannon 발산은 두 분포가 같을 때 0, 그리고 0보다 큰 값을 가지는 성질이 있다.

따라서 C(G) - (-log(4))는 0보다 크거나 같게되고, C(G)는 무조건 -log(4)보다 크거나 같게 되어 C(G)의 전역 최솟값이 -log(4)일 수 밖에 없게된다.

따라서 C(G)의 전역 최솟값은 pg = pdata가 되는 경우에 -log4를 가지며, 결국 생성모델(pg)이 정확하게 data 생성 process(pdata)를 복제해야만 최솟값을 가지게 되는 것이다.

 

2. Convergence of Algorithm 1

 

아래의 알고리즘 1을 살펴보자. 이는 minibatch SGD(Stochastic gradient descent) 학습 알고리즘으로, k는 하이퍼파라미터로서 작용한다. 

먼저 k회 만큼 반복되는 가장 안쪽의 반복문을 살펴보자.

• pg를 따르는 m개의 z를 미니배치 단위로 샘플링한다. 
• pdata를 따르는 m개의 x를 미니배치 단위로 샘플링한다.
• 판별모델을 이의 stochastic gradient를 ascending하는 방식으로 업데이트한다.

k회 만큼 판별모델을 업데이트하게 되면 다시 pg에서 z를 m개 단위로 미니배치 샘플링하고, 생성모델에 stochastic gradient를 descending하는 방법으로 생성모델 업데이트를 진행한다.

 

앞에서 얻어낸 pdata=pg 일 때, 전역 최적해가 존재한다는 사실을 알게 되었으니, 이제는 과연 이 알고리즘이 이러한 전역 최적해를 찾아낼 수 있는가를 확인해 보아야 한다.

 

Proposition 2. 만약 G와 D에 충분한 capacity가 존재하고, 알고리즘 1의 각 단계에서 판별모델이 주어진 G에 대한 최적값에 도달할 수 있으며, pg가 아래 수식을 개선하게 업데이트가 된다면, pg는 pdata로 수렴한다.

주어진 G에 대해 D*G(x)가 구해져 고정된 Value function V(G, D)

proof : V(G , D)에서 G는 pg에 dependent하므로 이 식을 U(pg, D)로 생각할 수 있다. pg가 gradient descending으로 더 나아지려면 k iteration만큼 D를 학습해서 얻어지는 D*G(X)가 주어졌을 때(즉 D가 고정된 상태), pg의 Value function인 U(pg, D)가 Convex형태여야 gradient descending으로 improve가 가능하다. 

위에서 언급한 V(G, D) 수식을 다시 가지고 왔다. 스티커가 붙여있는 아래의 수식을 보자. D(X)는 현재 고정되어 있는 상태이므로 이를 pg(x)로 미분하게 되면, log(1-D(x))만 남게되고, 이는 상수값으로, V(G, D) = U(pg, D)에서 D가 고정되어있는 경우 선형함수, 즉 주어진 구간 안에서 최솟값을 구할 수 있는 convex function이라고 할 수 있고 따라서 gradient descent 알고리즘으로 최적해에 다가갈 수 있음을 확인할 수 있다.

 

figure 1 : V(G , D) = U(pg, D)

그림을 통해 다시 살펴보자. V(G,D)는 위 그림에서 어느 지점에서 과연 전역 최적해를 가지게 될까? D 는 주어진 G에 대해 V(G,D)를 최대화 해야하고, G는 최적해 D*에 대해서 V(G,D)를 최소화 하려고 할 것이다. 각각이 이러한 방향으로 움직이게 되면, 이 알고리즘으로는 Nash Equilibrium 인 빨간점 즉 안장점(Saddle Point)에 최적해가 위치하게 될 것이다.

“The subderivatives of a supremum of convex functions include the derivative of the function at the point where the maximum is attained.”

논문에서는 이러한 표현을 사용하는데 이는 무엇을 의미할까?

 

모든 pg에 대해 D(x) = D*(x)로 고정시키고 Pg vs V(G, D)에 대한 그래프를 그리면 아래 그림과 같은 그래프가 얻어진다. 그래프의 각 점들은 pg가 주어졌을 때, inner loop(k 번 D 업데이트)에서 D에 gradient descent가 진행되며 얻어질 수 있다. 

 

figure 2:  pg vs V(D*, G) which is convex function

 

결국 논문에서 의미하는 바를 간단히 얘기하면, V(D*, G)의 pg에 대한 미분값들의 집합을 얻게 되면, 이 집합은 V(D,G)에서 주어진 pg에 대해 V(D,G) 값이 최대가 되는 지점의 pg에 대한 편미분값들을 모두 포함한다. 즉 figure 1의 안장점에서의 도함수는 figure 2에서의 도함수 집합의 어딘가에 존재한다는 것이다.

 

그리고 G(z)의 파라미터들에 gradient descent를 진행하면(V(D*, G)의 pg에 대한 편미분), pg를 업데이트할 수 있고, 안장점에 도달할 수 있다. 추가로 이전의 수학적 증명에서 pdata=pg, D(X)=1/2에서 global optimum을 얻는 다는 것을 알고 있으므로 증명이 완료된다.

 

다시 figure 1을 보자. 

 주어진 pg에 gradient descent를 적용하면, pg에 대한 optimum D를 얻을 수 있다.(알고리즘 1의 inner loop).
다음으로 D(x)를 고정시키고, pg에 gradient descent를 진행하면서, 안장점에 가까워 질 수 있다.
optimum D에서의 pg에 대한 미분 값이 안장점에서의 pg에 대한 편미분 값 을 포함하므로, D와 G에 충분한 capacity가 존재한다면, 위와 같은 알고리즘으로 안장점에 도달할 수 있다. 

실제 사용에서는 adversarial net이 G(z ; θg)로부터 나온 제한된 집합의 pg 분포를 나타내며, 증명에서 사용한 것처럼 pg를 optimize하는 게 아닌 θg를 업데이트 하게 된다. 멀티 레이어 퍼셉트론을 통해 G를 정의하는 것은 파라미터 공간에서 여러개의 극점(단 하나의 optimal solution을 뽑아내지 못함)을 제안하게 되지만, 이러한 이론적 한계에도 불구하고, 실제 사용에서는 굉장히 훌륭한 퍼포먼스를 냈다고 한다.

 

 

Experiments

논문에서는 MNIST를 포함한 다양한 데이터 셋에 adversarial net을 적용했다. 생성모델에는 ReLU와 sigmoid를 사용하고, 판별모델에서는 maxout 활성화 함수를 사용하였다. 판별함수에 dropout을 사용했다. 이론적 프레임워크 상으로는 생성모델에도 dropout이나, 중간 레이어에 noise를 추가하는 것도 가능은 했지만, 생성모델의 가장 처음 레이어의 input으로만 사용했다.

 

추정된 확률분포에 대해서는, pg가 직접적으로 추정되는 것이 아니므로 이를 근사할 수 있는 평가지표인 *Gaussian Parzen window를 사용했고. 

Gaussian Parzen window : 비모수 확률분포를 추정하기 위한 방식, 점 x를 중심으로 하는 hxh window를 띄우고, 그 안에 있는 샘플의 개수를 새는 방법으로 확률분포를 추정한다.

d차원의 경우 다음과 같이 표현된다.

이렇게 추정된 확률분포를 통해 Adversarial nets를 데이터셋(MNIST, TFD)에 평가한 결과를 확인해보면, 

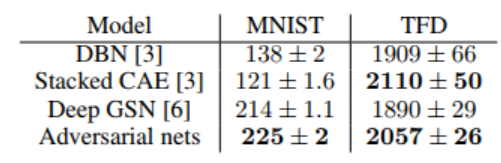
분산이 높고, 고차원 이미지(TFD)에 잘 수행되지 않았다. 논문에서는 오히려 이렇기 때문에, 추가 연구에 대한 동기부여가 제공된다고 한다.

위 그림은 GAN 모델로 부터 나온 샘플들을 가시화 한 것이다. 각 그림의 가장 오른쪽 노란색 태두리친 그림들이 생성된 샘플들이며, 이웃한 이미지(노란 테두리 바로 옆 이미지)에 대해 가장 가까운 분포를 가진 이미지를 얻어낸 것이다.

위 그림은 Full model의 z(input noise)공간상에서 두 지점 사이를 interpolating(보간)하는 방식으로 생성해낸 데이터이다.

위 두 그림에서 보다시피, metrics(Gaussian parzen window)측면에서는 부족하더라도 우리가 시각적으로 보기에는 굉장히 그럴듯한 결과가 나오는 것을 확인할 수 있었다.

다양한 모델을 비교한 Table

위 테이블을 보면 다양한 생성모델을 비교한 것인데, 여기에서만 보면, Adversarial model이 p(x)를 직접 추정하는 것이 아니라는 것이 한계로 보인다.

 

Advantages and disadvantages

장점:

• 마코브체인이 필요하지 않음
• gradient를 얻기 위해 backpropagation만 필요(학습 중 inference(추론)과정이 필요하지 않음)
• 다양한 functions을 모델에 통합 가능

단점:

• pg(x)를 명시적으로 추론하지 않음.(멀티레이어 퍼셉트론에서의 θg를 추론)
• D가 학습과정에서 G와 잘 맞아야함 (D가 충분히 학습되지 않은 상태에서 G의 학습이 많이 진행하게 되버리면 local minima로 빠지는 Helvetica scenario에 도달할 수 있음.) Mode collapse라고도 함.

 

 

 

 

 

References: 

쿨백-라이블러 발산, 교차엔트로피(cross entropy)

 

[논문리뷰]GAN(Generative Adversarial Nets) 리뷰

Generative Adversarial Networks — A Theoretical Walk-Through.

5-2.GAN (Part2. Theoretical Results)