고정 헤더 영역
상세 컨텐츠
본문

작성자 : 채윤병
1. Introduction
하나의 그래프에서 노드에 label이 일부분만 주어질 때 노드를 분류하는 문제를 Graph-based semi-supervised learning이라고 한다. 이 경우 label에 대한 정보가 smoothing 될 수 있다.

L0 - supervised loss
Lreg - regularization term
△ = D - A → Unnormalized graph Laplacian of undirected graph
Eq.1의 가정 : 그래프에서 연결된 노드는 같은 label을 가질 가능성이 높다. (그러나 이러한 가정은 model의 capacity를 제한할 수 있는데, graph의 edge는 node의 similarity 뿐만 아니라 부가적인 정보를 담을 수 있기 때문)
Lreg에서 adjecency matrix로 conditioning을 하는 것의 역할
- Supervised loss L0에서의 gradient를 모델에 분배
- Node에 label이 없더라고 representation을 학습할 수 있다.
Paper의 Main contribution
- 그래프에 직접적으로 적용할 수 있는 간단하고 잘 동작하며 neural network 모델을 위한 propagation rule을 소개하고 spectral graph convolution의 1차 근사에 어떻게 motivated 했는지 설명했다.
- 해당 graph-based neural network 모델이 빠르고 scalable하게 semi-supervised classification문제에 사용되는 것을 보였다.
2. Fast Approximate convolution on graphs

A hat - Adjacency matrix with added self-connections
D hat - Node degree(diagonal matrix)
W - Weight matrix
Activation function - ReLU
Main idea : 정규화를 통해서 edge 개수와 관계없이 학습이 잘 되도록 하고 이를 Hidden representation과 곱하여 이웃 노드의 represenation의 가중합을 만들고 이를 학습 가능한 W와 곱함.(인접 노드들의 가중치 * feature vector * weight)
이 Layer를 k개 쌓으면 k hop neighbor까지의 정보를 고려할 수 있다. 또한 node label이 적더라도 representation을 학습할 수 있다
2.1 Spectral Graph Convolutions

U - Normalized graph Laplacian의 eigenvector matrix
UTx : Graph Fourier transform of x
Spectral convolution : Laplacian의 eigendecomposition의 결과(U∧UT)와 x를 곱한 것
Large graph에서 Laplacian의 eigendecomposition을 하는 것이 오래 걸려서 Chebyshev 다항식을 사용해 근사하는 방식을 사용했다. (First order approximation, k = 1)
2.2 Layer-wise Linear Model
k = 1이기 때문에 graph Laplacian spectrum에서 linear function이다.
Layer-wise한 형태로 인해서 여러 layer를 stacking 할 수 있고, modeling capacity를 늘릴 수 있다.

괄호 안의 행렬을 반복적으로 사용하는 것은 두 가지 문제를 야기할 수 있다.
- Numerical instabilities
- Exploding/vanishing gradients when used in deep neural network model
이를 해결하기 위해 renormalization trick을 사용

해당 방법을 사용하면 Eigendecomposition을 직접할 때보다 연산량을 효율적으로 줄일 수 있으므로 큰 그래프에서도 적용하기에 용이하다.
3. Semi-supervised Node Classification
A conditioned neural network{ f(X, A) }의 도입을 통해서 data X에 없는 정보를 A가 가지고 있을 경우(citation network에서 document의 citation link 또는 knowledge graph에서의 relations) 효과적이다.


레이블이 있는 데이터에 대해서만 cross entropy loss를 통해 loss 계산
6. Results


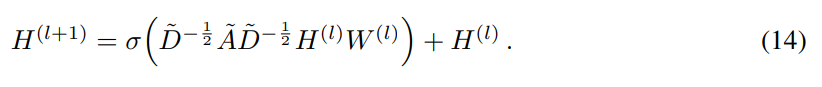

7-8. Discussion & Conclusion
기존의 graph-Laplacian regularization을 사용한 방법은 edge가 단순히 node의 similarity를 encoding 하고 있다는 가정 때문에 model capacity의 제약이 있었으며, Skip-gram 기반의 모델들은 random walk generation과 semi-supervised training의 최적화를 동시에 할 수 없다는 약점이 있었다.
그러나 이를 GCN의 Loss term에서 해결했다!
Renormalized propagation model을 도입하여 적은 파라미터로도 효율적으로 모델의 예측력을 높일 수 있었다.
이후 개선해야할 점
- Memory requirement
- Directed architecture(DAGNN - ICLR2021)
- Limiting assumptions - Equal importance self connections
참조 :
https://baekyeongmin.github.io/paper-review/gcn-review/
(Normalization)
Graph Convolutional Networks Review
이번 EMNLP 2019에서 Graph Neural Network(GNN) 튜토리얼 세션이 진행되었습니다. 그 중 가장 처음으로 소개되었던 Semi-Supervised Classification with Graph Convolutional Network(ICLR 2017)을 살펴보고자 합니다. 본 논문
baekyeongmin.github.io
https://m.blog.naver.com/winddori2002/222183504185
(코드 리뷰)
[바람돌이/딥러닝] GCN 논문 및 코드 리뷰 (Semi-Supervised Classification with Graph Convolutional Networks)
안녕하세요. 오늘은 graph-structured data를 활용하여 semi-supervised learning을 적용한 GCN 논문 내...
blog.naver.com
'심화 스터디 > Graph Study' 카테고리의 다른 글
| [Graph 스터디] DAGNN(Directed Acyclic Graph Neural Networks) (0) | 2022.11.23 |
|---|---|
| [Graph 스터디] Neural Message Passing for Quantum Chemistry(MPNN) (0) | 2022.11.02 |
| [Graph 스터디] Graph Neural Network (0) | 2022.10.09 |
| Predict then propagate : Graph Neural Network meet Personalized PageRank (0) | 2022.09.22 |
| Graph neural network review(2) (0) | 2022.09.13 |





댓글 영역