[Advanced ML & DL Week 5] Long Short-Term Memory

작성자: 15기 조우영

Introduction

• 목적: Sequential data를 학습하기 위해 기존의 RNN 구조는 시간이 오래 걸리거나 vanishing gradient, exploding gradient 때문에 학습이 정상적으로 진행되지 않는 문제들을 보완한 모델인 LSTM을 소개하고자 함
• 선행 연구들
  • Gradient-descent variants: time step이 커지면서 vanishing/exploding gradient 발생
  • Time-delays: long term에 대해서는 효과적이지 않음
  • Time constants: long term에 대해서는 효과적이지 않고, 별도의 tuning을 요구함
  • Ring’s approach: time step이 늘어날 때마다 그만큼 unit의 수도 늘어나고, generalize가 잘되지 않음
  • Bengio et al.’s approaches: 특정한 문제들을 해결하기 위해서 말도 안되는 수의 states가 요구됨
  • Kalman filters: long term에는 효과적이지 않음
  • Second order nets: long term에는 효과적이지 않고 LSTM은 매 step에서 시간 복잡도가 O($w$)인 반면 second order nets는 O($W^2$)임
  • Simple weight guessing: 단순한 방법으로 일부 task에 대해서는 좋은 성능을 보이나 언제나 적용가능한 좋은 알고리즘은 아님
  • Adaptive sequence chunkers: noise level이 증가하거나 input sequence가 compressible하지 않으면 성능이 저하됨
• Vanishing Gradient란??

https://en.wikipedia.org/wiki/Sigmoid_function, https://www.google.com/search?q=tanh+function&rlz=1C5CHFA_enKR970KR970&sxsrf=ALiCzsZMARS1qlOd5MxQpC0XvFSw5zvSkw:1668095468966&source=lnms&tbm=isch&sa=X&ved=2ahUKEwih5oPv-6P7AhX1l1YBHe8EC6kQ_AUoAXoECAIQAw&biw=1638&bih=803&dpr=2#imgrc=z32UBMVB7ANzOM, https://excelsior-cjh.tistory.com/177

 

https://www.baeldung.com/cs/sigmoid-vs-tanh-functions

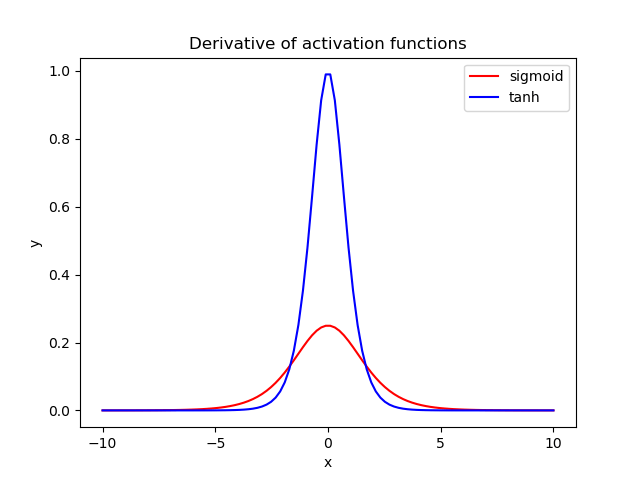
우리가 흔히 많이 쓰는 활성화 함수인 Sigmoid는 미분값의 범위가 0부터 최대 0.25까지고, tanh 같은 경우에는 0부터 최대 1까지의 값을 갖는다. 따라서 back propagation이 진행되면서 1보다 작은 값이 계속해서 곱해지게 되고, 이로 인해 gradient가 제대로 전달되지 못하고 0으로 수렴해 소실되는 현상을 의미한다. 

 

• Exploding Gradient란?

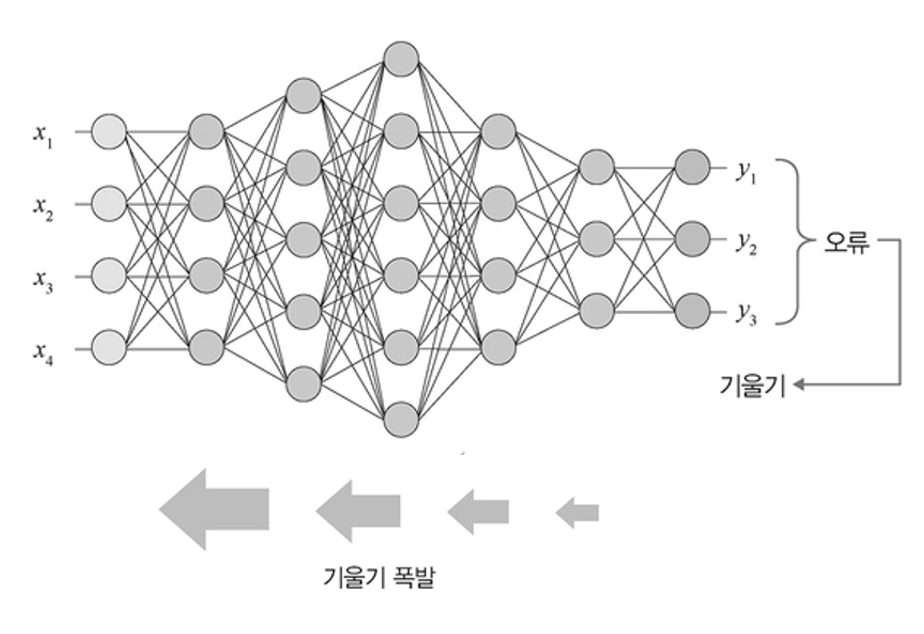
Vanishing Gradient와는 정반대의 상황으로, 기울기의 절대값이 1이 넘는 활성화 함수를 사용 시, 절대값이 1보다 큰 값이 계속해서 곱해져, 이로 인해 gradient가 비정상적으로 커지는 현상을 의미한다. 

 

 

RNN

 

앞으로 소개할 LSTM도 RNN구조의 한 종류이고, 기존 RNN구조(Vanilla RNN)의 문제들을 보완하기 위해 새로 제시된 모델이기 때문에 RNN에 대해 먼저 간단히 소개하고 넘어가겠다. 

• 등장 배경: RNN 이전 기존의 neural network들은 모든 input들이 서로 독립이라는 가정을 하기 때문에 사건들이 특정한 순서를 가지고 순차적으로 벌어지는 sequential data들을 처리하기에 부적합하기 때문에 sequential data를 다루기에 적합한 모델을 만들고자 함
• IDEA: 이전 셀의 output을 다음 셀의 input으로 사용하여 이전 셀들에 대한 정보들을 계속하여 미래로 넘겨주자

RNN 구조

input이 hidden layer를 통과하면서 output으로 향함과 동시의 다음 state의 hidden layer에 다시 들어가는 구조를 통해 순서를 가지고 순차적으로 벌어지는 sequential data들을 처리하고 있다.

 

RNN에 대한 보다 자세한 설명은 

https://wikidocs.net/22886

1) 순환 신경망(Recurrent Neural Network, RNN)

https://www.youtube.com/watch?v=AsNTP8Kwu80 

등을 참고하면 좋을 것 같다. 

 

하지만, RNN은 Activation function으로 tanh 사용하기 때문에 몇 가지 문제가 발생하는데, 

1. Forward 연산 시: tanh는 -1과 1 사이의 값을 가지기 때문에 이 값이 반복적으로 곱해지면서 앞의 정보가 뒤로 충분히 전달되지 못해 짧은 sequence에 대해서만 효과를 보인다. 이를 장기 의존성 문제(Long-term Dependency)라고 부른다.
2. Back propagation시: tanh의 미분값은 0과 1 사이의 값을 가지기 때문에 0과 1사이의 값이 반복적으로 곱해지면서 vanishing gradient 문제가 발생한다.

 

그리고 이런 문제들을 보완하기 위해 고안된 것이 Long short-term memory, LSTM이다.

 

 

* 여기서 개인적으로 한 가지 의문이 들었는데, Activation function으로 tanh 사용하기 때문에 문제가 발생한다면, 어렵게 새로운 구조를 생각해내는 것보다는 ReLU activation function을 사용하면 간단히 해결이 되지 않을까?하는 의문이었다.

이에 대한 답은, ReLU는 상한선이 존재하지 않는 활성화 함수이기에, forward 연산 시 값이 너무 커지는 문제가 발생해 RNN 구조에서 잘 사용되지 않는다고 한다. 

 

LSTM(Original LSTM)

 

• 등장 배경: 기존 RNN 모델보다 vanishing/exploding gradient에 대해 덜 민감하며 긴 time step에도 학습이 가능한 모델을 만들고자 함
• IDEA: 장기기억 cell 구조 도입, Gate 구조 도입, Training method 개선

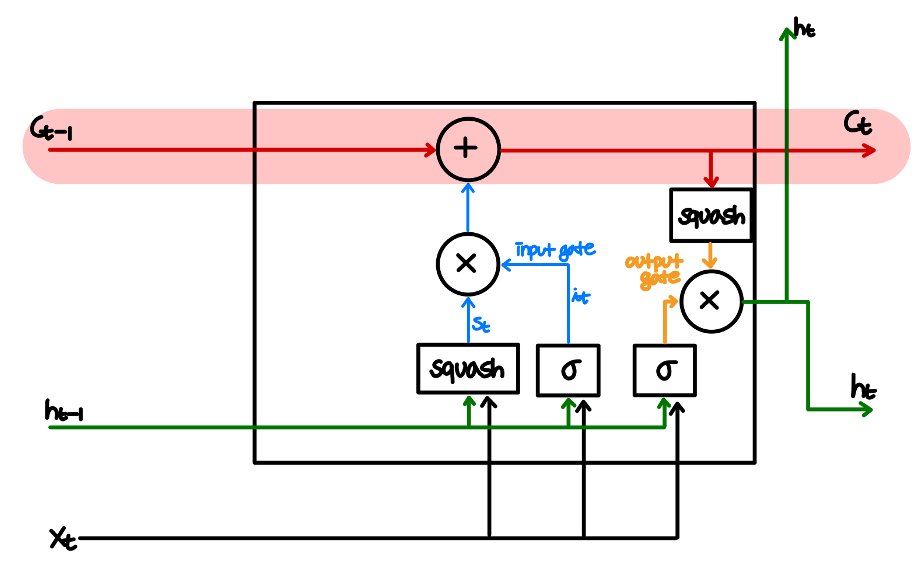
1. 장기적인 cell 구조 도입

cell state에는 더하기 연산만 존재하기 때문에 backpropagation시의 정보 손실이 존재하지 않아 vanishing gradient가 발생하지 않고 더 긴 time 학습이 가능하고, 이를 계속 뒤로 넘겨주는 것으로 RNN에서 forward 연산 시에 발생하던 장기 의존성 문제 또한 해결이 가능하다.

   

 

    2-1. Gate 구조 도입-Input Gate

 

 

이전 unit의 출력값인 $h_{t-1}$과 $x_t$를 입력으로 받아 이에 activation function을 적용한 값 $s_t$에 0과 1사이의 값을 갖는 $i_t$를 곱하여 장기기억 cell에 현재와 바로 직전 정보에 대한 업데이트 비율을 결정함

수식으로는 다음과 같이 표현된다. 

 

 

 

 

 

 

 

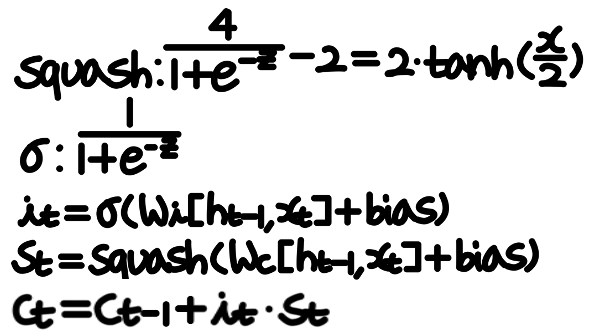
* 참고: 왜 tanh가 아닌 tanh의 변형인 Squash function을 사용했을까? 

tanh와 squash function을 미분하면 위와 같은 형태를 띄는데, Squash function이 좀 더 넓게 퍼져있는 것을 볼 수 있다. Squash function의 이런 구조가 vanishing gradient 문제에 대해 tanh function보다 덜 취약하기 때문에 변형을 하여 사용한 것으로 보인다.

 

 

    2-2. Gate 구조 도입-Output Gate

 

 

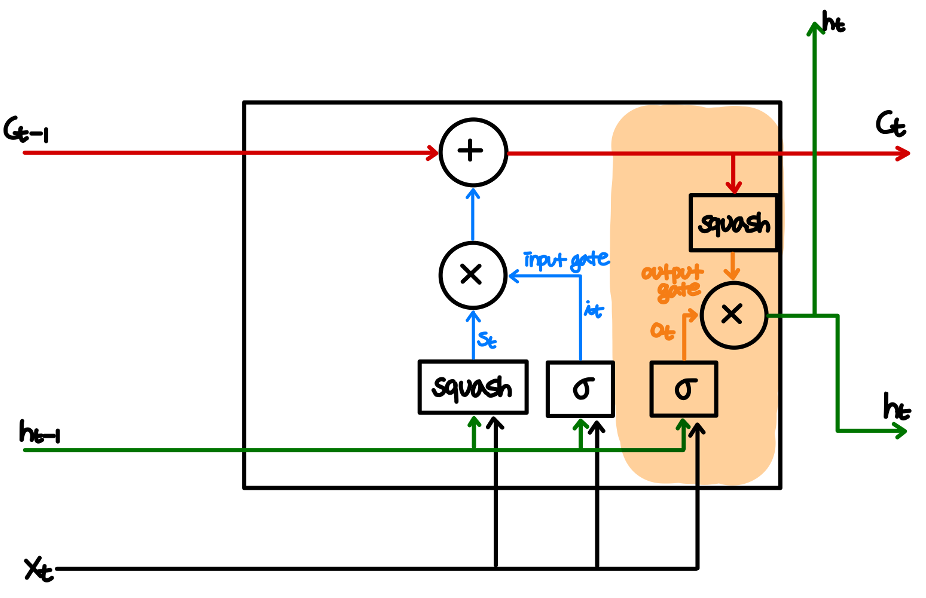
Cell state에 squash activation을 하고 이에 0과 1사이의 값을 곱하는 방식으로, cell state를 이용하여 다음 출력값이 될 $h_t$를 결정

* 지금까지에 대해 보다 완전한 정보를 갖고 있는 $c_t$에서 일부 정보만을 필터링하여 현재 time step에 직접적으로 필요한 정보만을 갖도록 하는 것으로 이해할 수 있다. 

수식으로는 다음과 같이 표현된다. 

 

 

 

 

 

그런데, 앞서 ReLU를 사용하지 않은 이유가, 상한선이 존재하지 않는 활성화 함수이기에, forward 연산 시 값이 너무 커지는 문제가 발생하기 때문이라 했는데, 이건 단순히 더하기 연산만을 반복적으로 수행하는 cell state도 마찬가지가 아닌가? 맞다. 그래서 이를 해결하기 위해 forget gate라는 하나의 gate가 추가된 LSTM 모델이 후에 고안되었는데, 이것이 현재는 Vanilla LSTM으로 굳어져있다. 추가로, 앞서 언급한 squash function의 구조가 tanh function보다 이러한 문제에 취약하기 때문에 Vanilla LSTM에서는 tanh를 사용한다. 

 

 

Vanilla LSTM

 

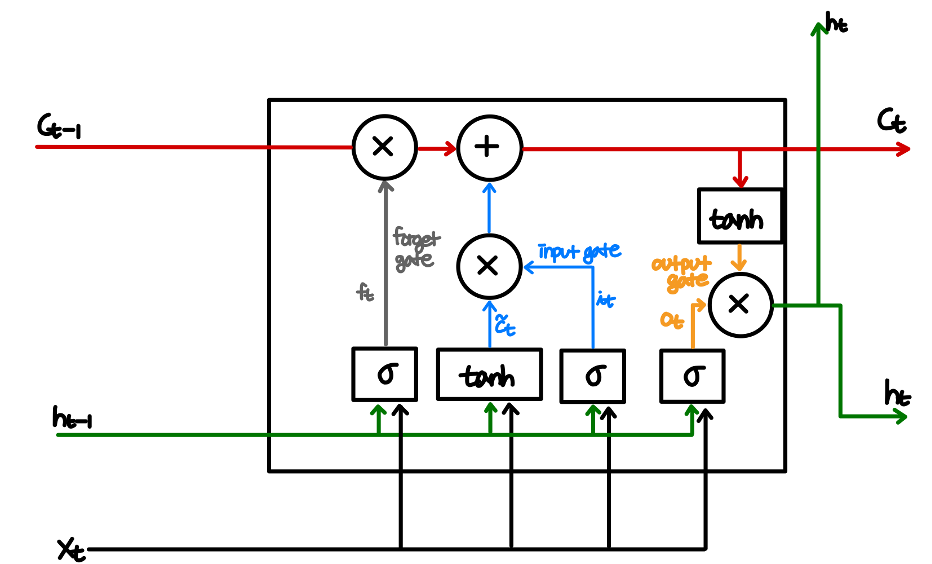
• Forget Gate: Original long term memory(기존의 cell state) 중 얼마나 기억할지(다음 state으로 옮길지) 결정
• Input Gate: Potential long term memory(현재 새로 입력받은 값) 중 얼마나 기억할지 결정
• Output Gate: 다음 hidden state의 값을 결정

 

 

 

 

 

 

 

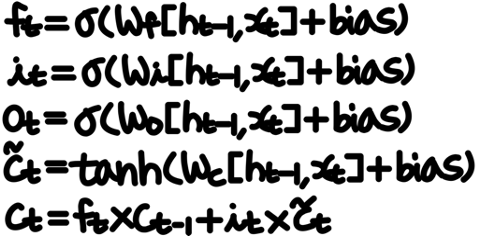
그런데 sigmoid 활성화 함수를 이용하는 forget gate를 사용하면 다시 vanishing gradient 문제가 발생하지 않을까?

실제로 발생한다. 하지만 LSTM 구조에서는 sigmoid 활성화 함수를 cell state에 직접 적용하는 것이 아닌 그 결과를 곱하는 것이기 때문에 덜 취약하고, 추가로 뒤에 input gate를 통해 구해진 값이 더해지기 때문에, forget gate를 통해 구해지는 값과 input gate를 통해 구해지는 값이 상호 보완적으로 어느정도 이 문제를 완충시켜준다고 한다. 또한, weight의 값을 이용하여 forget gate의 sigmoid activation 결과 값이 1에 가깝도록 학습하는 것이 가능하기 때문에, vanishing gradient에 대해 기존 Vanilla-RNN보다 강한 모습을 보여주고, 1000개 time step 정도까지는 문제 없이 사용이 가능하다고 한다. 

 

 

참고 자료: 

https://www.youtube.com/watch?v=IgIHjiCgECw&t=1310s 

https://www.youtube.com/watch?v=YCzL96nL7j0&t=1089s 

https://wikidocs.net/22888

2) 장단기 메모리(Long Short-Term Memory, LSTM)