고정 헤더 영역
상세 컨텐츠
본문
작성자: 16기 이수찬
참고 영상: (1) (2022-02) Dive into Deep Learning 01. Introduction to Deep Learning - YouTube
https://www.youtube.com/playlist?list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi (해당 플레이 리스트 동영상 4개)
1. Neural Networks
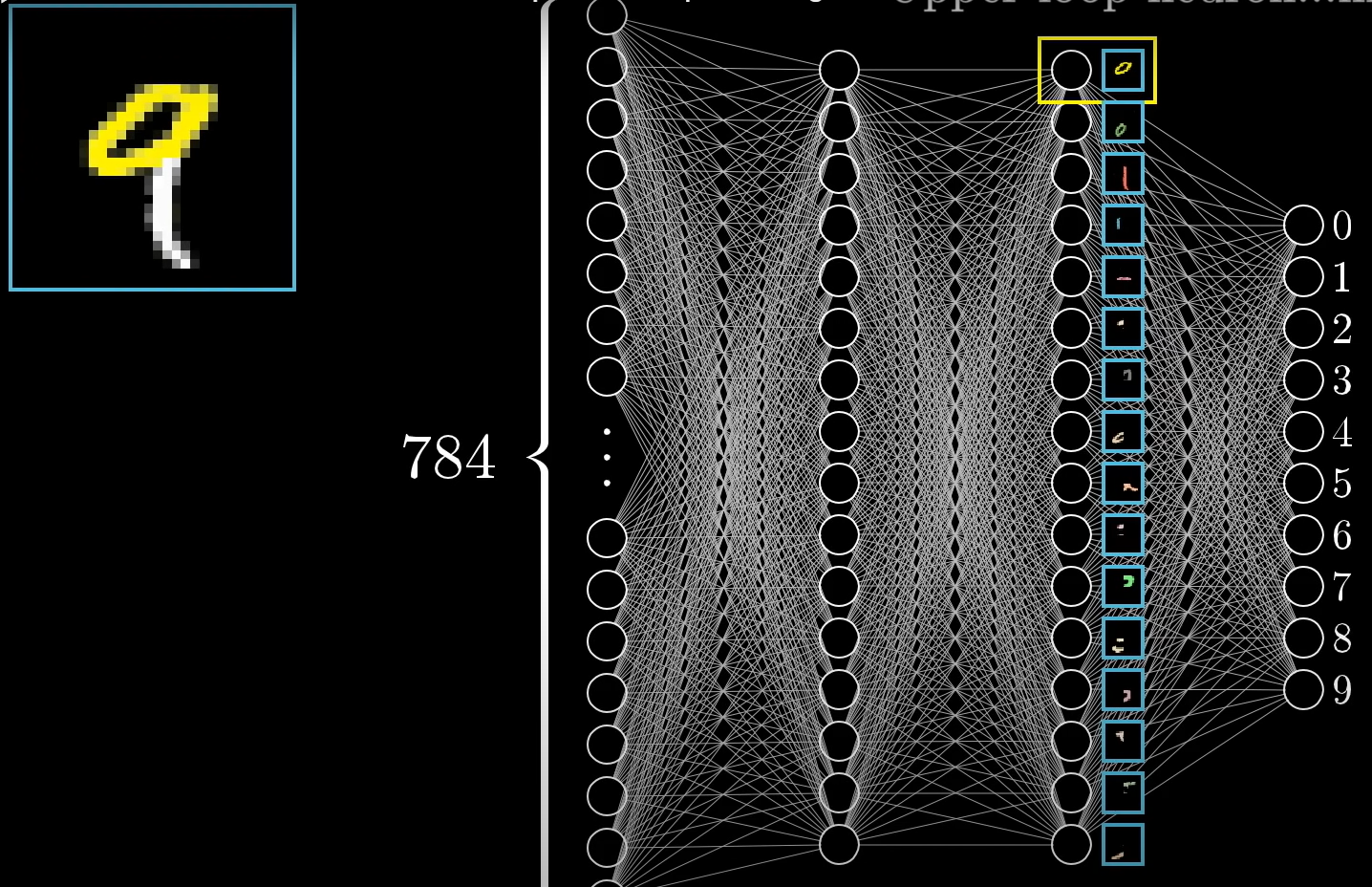
- Neuron: Each neuron represents a function where the output is decided based on the input number, in the case of number recognition example provided in the video, from the corressponding pixel.
- In the first layer of the neural network, there exists a neuron for each pixel in the input image. So in this case the entire neural network is basically a function that take in 784 numbers and outputs one out of a total of 10 possible outputs.
- As the original input progresses through the multiple layers in the neural network, weights and biases are utilized to group neurons representing a certain feature into one neuron that will represent the existence of the certain feature.
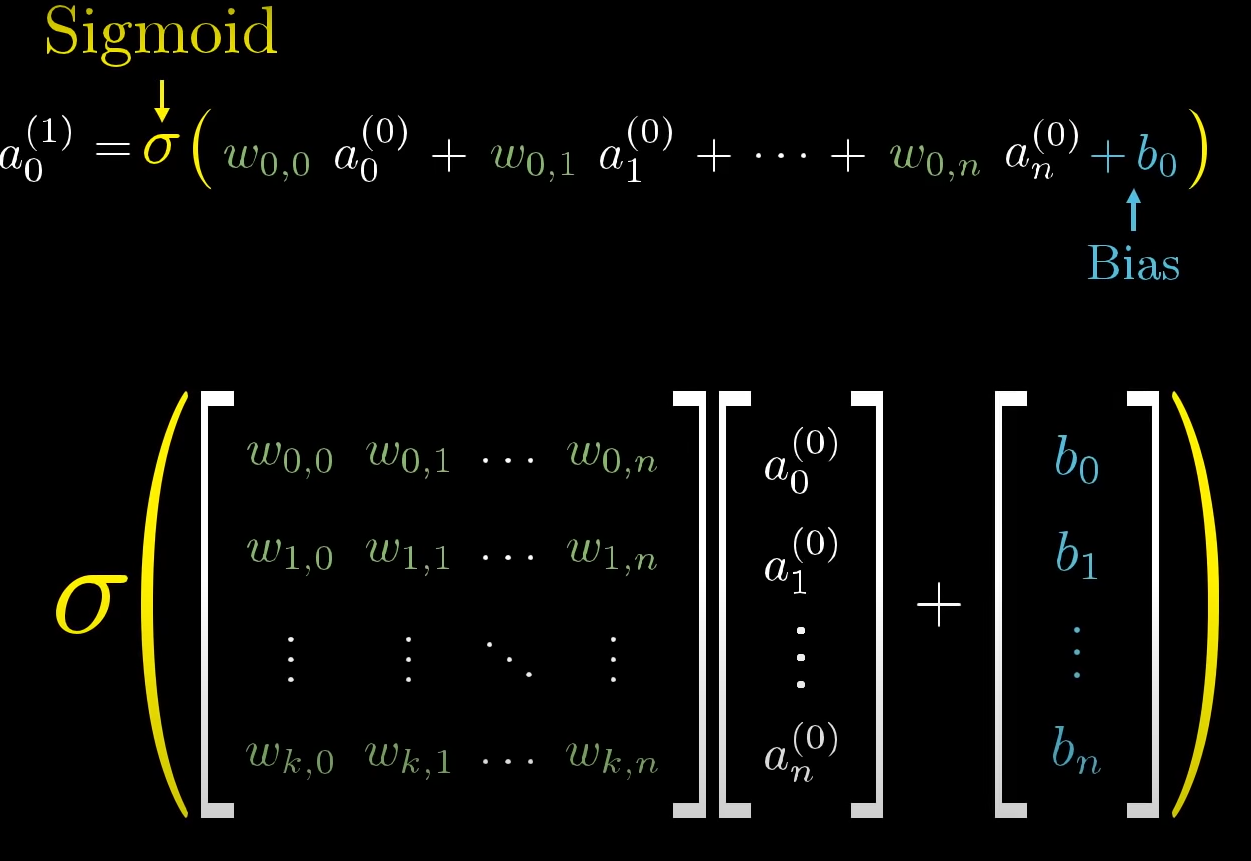
- The neural network can be represented as a mathematical function. The outputs of the fuction are put into the sigmoid function in order to represent activation and inactivation of the final neuron.
- There is an alternative to the sigmoid function called Rectified Linear Unit (ReLU) which is known to represent the activation of neurons more realistically.

2. How do Neural Networks Learn?
- Neural networks can 'learn' by tweeking its weights in the direction of minimizing the cost function using guided training.
- A cost function is the average of the sum of the squared difference between the output values of the neural network and the expected values.

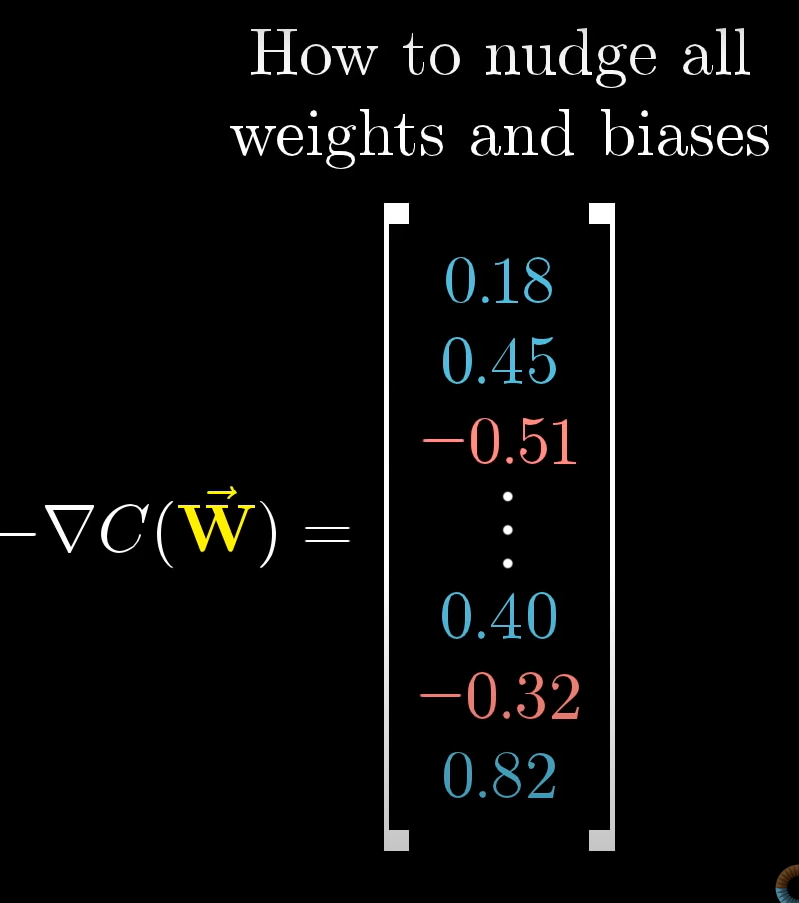
- Neural networks try to minimize the cost function by working towards the local minimum of the cost function using the negative of the gradient at a certain point it is at. This is called gradient descent.
- Gradient descent is used in the 'learning process' of the neural network

- The negative gradient of the cost function tells the neural network exactly in what direction and how much the weights should be changed.
3. Backpropagation
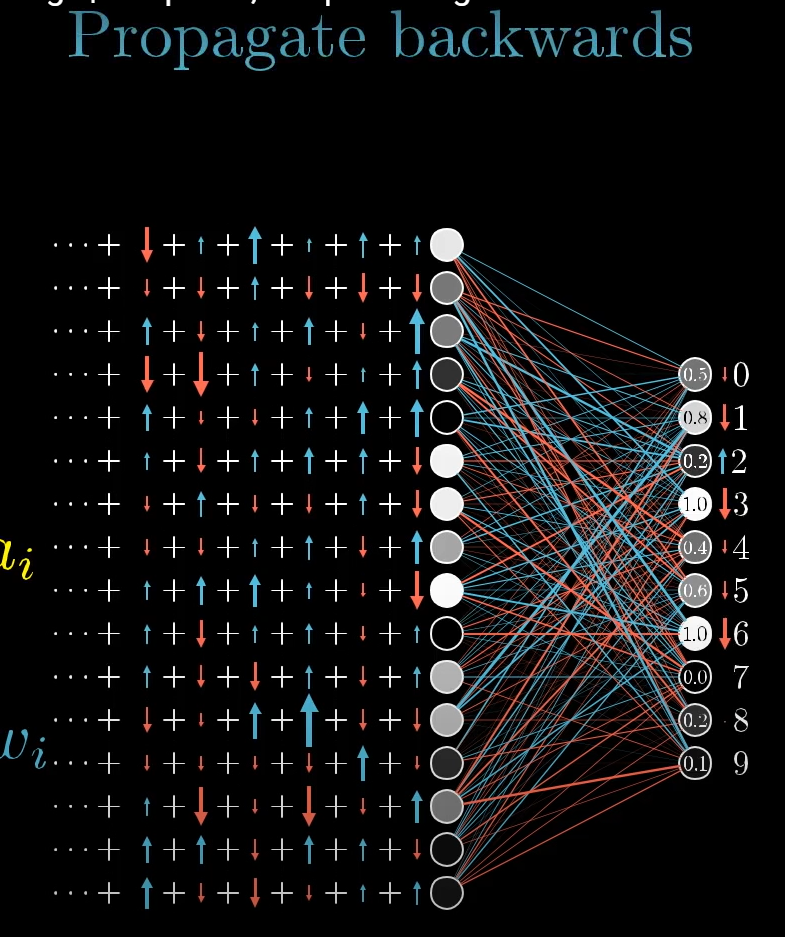
- The literal process of using the negative gradients of the cost function to make adjusts to the previous layer's weights and biases so that the cost function is minimized.
- The sizes of the 'nudges' that the weights receieve are proportionate to the absolute value of the gradient of the cost function.
- This process takes place 'backwards' going towards the previous layers from the final layers.
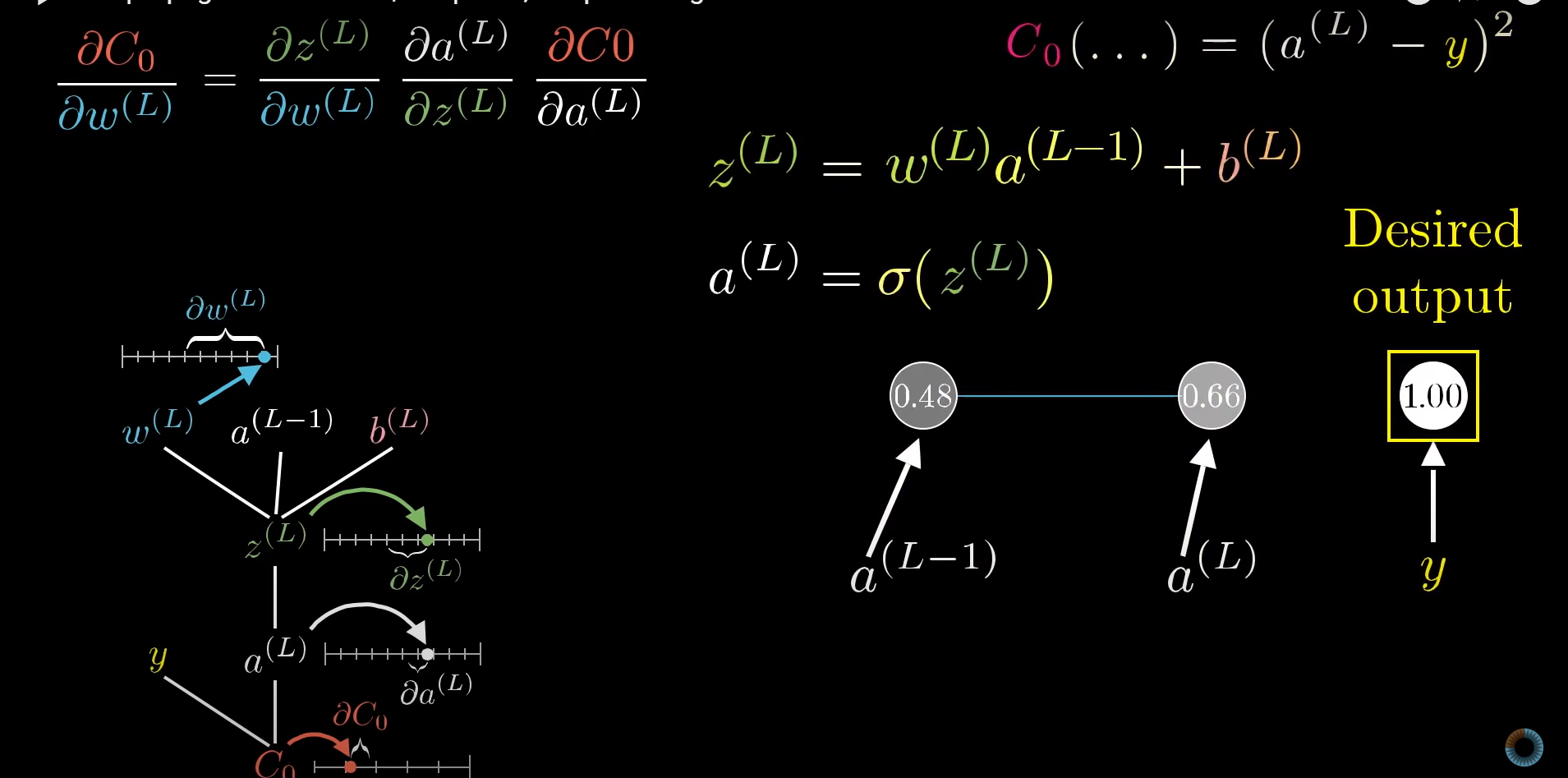
- When we look at a simple exmaple of a multi-layer neural network with one neuron in each layer, we can take a look at the math behind backpropagation.
- We want to see how sensitive the cost function is to chages in the weight of the connection between the two neurons.
- The nudge to the weight causes a change in the result of the function z(L) which represents the output from the connection between the two neurons before it is put into the sigmoid function. Then this change in z(L) causes the change in a(L) the final output of the neuron, changing the cost function.
- So the derivative of w(L) relative to the cost function can be find by using the chain rule to multiply the ratios of the three equations as shown below, which gives us the sensitivity of 'C' in relation to changes of w(L).
- The addition of more neurons to each layer just increases the number of indices that we must keep track of, but the overall mathematical concept does not change.
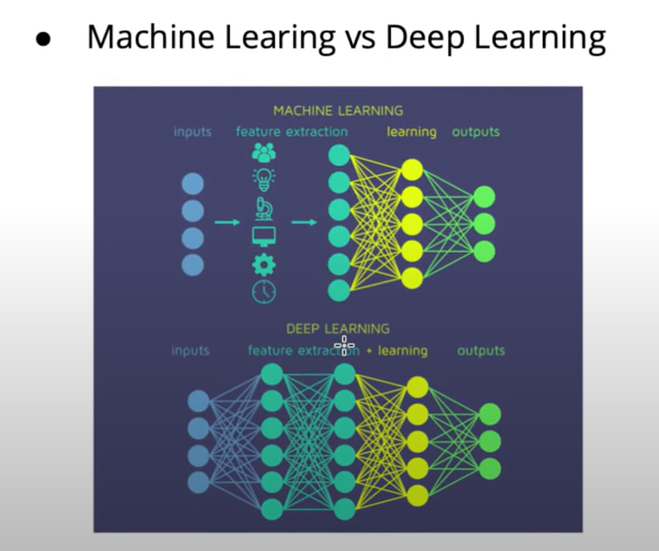
4. The Difference Between ML and DL
- In machine learning, the important features must be extracted manually and through a feature engineering process by the data scientist.
- In contrast, deep learning assumingly automates the process of feature selection making it an end to end learning process.
'심화 스터디 > Dive into Deep Learning' 카테고리의 다른 글
| [Dive into Deep Learning / CNN] Fully connected layer / pooling layer (0) | 2022.11.13 |
|---|---|
| [Dive into Deep Learning / 3주차] Python Class (2) | 2022.09.30 |
| [Dive into Deep Learning / 2주차] Backward Function Problem (0) | 2022.09.25 |
| [Dive into Deep Learning / 2주차] PyTorch Automatic Differentiation (1) | 2022.09.25 |
| [Dive into Deep Learning / 2주차] Tensor Manipulation (0) | 2022.09.25 |





댓글 영역