고정 헤더 영역
상세 컨텐츠
본문 제목
[Advanced ML & DL Week2] Probabilistic Latent Semantic Analysis
본문
작성자: 15기 조우영
Introduction
인간의 언어를 이해하는데에 있어서 machine learning system이 직면하는 근본적인 문제는 특정 데이터에서 단순히 사용된 언어와 실제로 언어가 어떠한 의미를 담고있는가를 구별하는 문제이다. 이러한 문제의 원인은 크게 2개로 분류될 수 있는데,
- Synonymy: 똑같은 개념을 표현할 수 있는 다양한 단어들이 존재
- Polysemy: 한 단어에도 다양한 의미가 존재
이다.
이러한 문제를 해결하기 위한 방법으로 잘 알려진 방법이 Latent Semantic Analysis(LSA, 잠재의미구조분석)이다. 이름에서 알 수 있듯이 LSA의 목표는 단순한 단어의 수준을 뛰어 넘는 정보를 제공하고 사용자가 실제로 관심을 가지고 있는 토픽과의 의미 관계를 나타내는 데이터 매핑을 찾는 것이다. LSA의 핵심은 고차원의 term-document matrix를 저차원의 latent semantic space로 표현하는 것이다. LSA는 광범위한 응용 분야에서 유용한 분석 도구이지만, 그 이론적 토대는 아직 불완전하다. 따라서 일반적인 LSA와 달리 좋은 통계적 기반을 가지고 있으며 데이터의 적절한 생성 모델을 정의 가능한 새로운 방법인 PLSA를 제시하고자 한다.
Latent Semantic Analysis
Count Data and Co-occurrence Tables
Vocabulary $W =$ {$w_{1}, w_{2}, ..., w_{M}$}에 속하는 term들로 이루어진 document 집합 $D =$ {$D_{1}, D_{2}, ..., D_{N}$}이 주어졌다고 가정하자. 단어 발생의 순서를 무시하면, 해당 데이터를 N X M의 테이블로 표현할 수 있다. 테이블의 i, j번째 cell은 $N = (n(d_{i}, w_{j}))_{ij}$를 값으로 갖고, 해당 기호는 term $w_j$의 document $d_{i}$에서의 발생 횟수를 의미한다. N은 term-document matrix라고도 불리며, 다음과 같은 형태를 지닌다.
* Vocabualry란? 텍스트의 모든 단어를 중복 없이 모아놓은 서로 다른 단어들의 집합

- Terms에 등장한 index terms는 한 개 이상의 문서의 제목에 등장한 단어들이다.
- c1~c5는 human-computer interaction과 관련된 문서들이고, m1~m4는 graph theory와 관련된 문서들이다.
- 각 cells는 각 문서의 제목에서 해당 단어가 등장한 횟수이다.
Latent Semantic Analysis by SVD
모든 rectangular matrix(t x d matrix, t for terms, d for documents)는 다음과 같은 3 matrices의 곱의 형태로 표현될 수 있는데 이를 X의 singular value decomposition이라 부른다.
$X = T_{0}S_{0}D_{0}'$
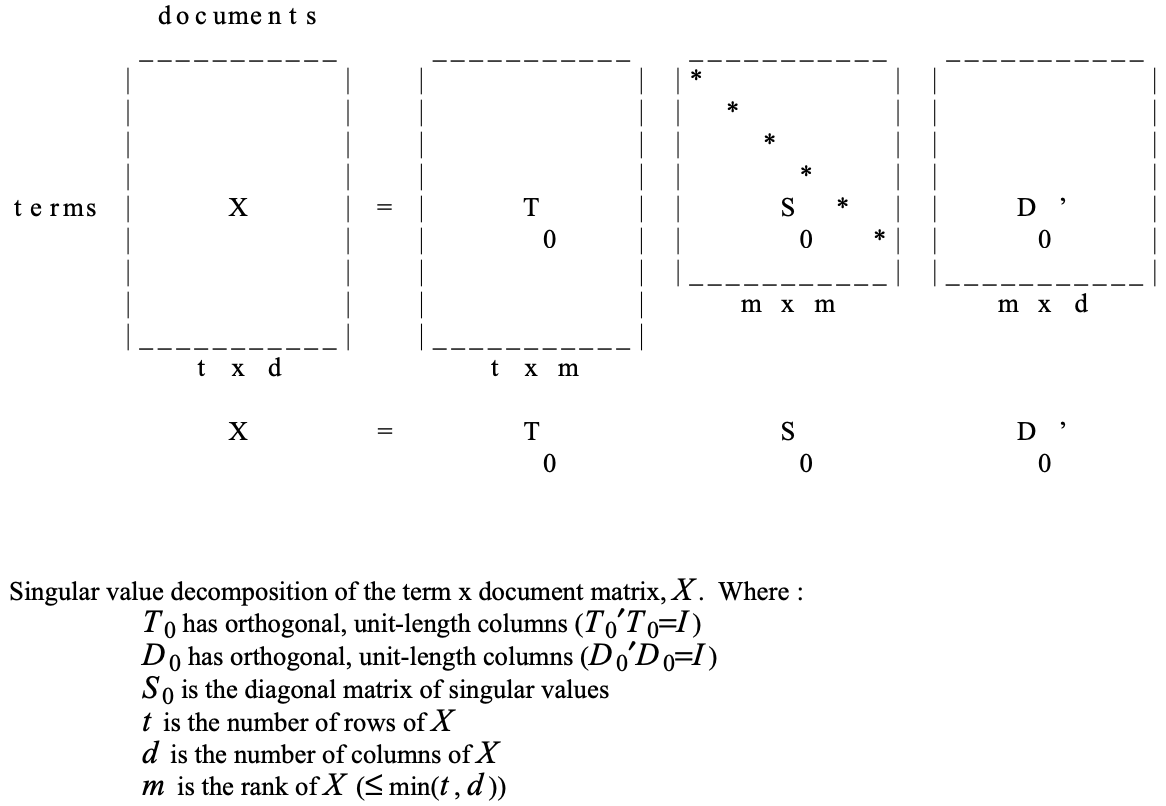
- $T_{0}$와 $D_{0}$는 orthonomal(column vector들의 inner product가 0, 모든 벡터의 크기가 1)한 column들을 가지고 $S_0$은 diagonal matrix이다.
- $T_{0}$와 $D_{0}$는 각각 left singular vectors, right singular vectos로 구성된 행렬이고, $S_{0}$는 singular values로 구성된 diagonal matrix이다.
- SVD의 결과는 row, column, sign permutation까지 모두 unique하다. 통상적으로, $S_{0}$의 원소는 모두 양수이고, 크기에 따른 내림차순으로 배열될 수 있게끔 구성한다.
- 일반적으로, $T_{0}, S_{0}, D_{0}$ 모두 full rank이다.

- SVD의 강력한 이점은 더욱 작은 행렬을 이용하여 최적의 근사를 하는 방법이 간단하다는 것이다. $S_{0}$의 singular values 중 k largest singular values는 유지하고, 나머지는 0으로 만든다. 이렇게 새로이 만든 $S_0$와 $T_{0}, D_{0}$의 product로 표현되는 새로운 행렬 $\hat{X}$는 rank k를 갖는 X의 근사행렬이 된다.
* 이 때 k는 가장 좋은 검색 성능을 보이는 k를 사용한다.
- 위의 과정에서 $S_0$의 밑부분에 zeros를 남겨놓았기 때문에 $S_{0}$는 diagonal matrix가 아니다. 이 zero rows를 delete하고 일부 columns를 delete함으로 $S_0$에서 새로운 diagonal matrix S를 만들 수 있다. $T_0$와 $D_0$의 대응하는 columns를 delete해 새로운 matrix T와 D를 만들어내면 다음과 같은 reduced model을 얻을 수 있다.
$X$ $\approx$ $\hat{X}$ = $TSD'$


위의 그림을 다시 살펴보자면, k를 사용자가 원하는 잠재의미의 수라고 표현한다고도 한다. Reduced model의 축소된 T는 t × k의 크기를 가지는데, 이는 잘 생각해보면 단어의 개수 × 잠재의미의 수의 크기이다. 이는 t개의 단어를 잠재의미를 이용하여 나타내고 있는 것으로도 해석이 가능하다. 즉, T의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 단어 벡터라고 볼 수 있다. 마찬가지로 $D^{T}$는 k × d의 크기를 가지는데, 이는 잠재의미의 수 k × 문서의 개수의 크기이다. 따라서 $D^{T}$의 각 열은 잠재 의미를 표현하기 위해 수치화된 각각의 문서 벡터라고 볼 수 있다.
이를 통해 사용자는 문서에 공통된 용어가 없더라도 문서 쌍 간의 의미 있는 연관 값을 계산할 수 있었다.
LSA에 대한 자세한 내용은 이곳에서 확인할 수 있다.
Probabilistic LSA
The Aspect Model
Aspect model이란 관찰되지 않는 class variable $z \in Z = $ {$z_{1}, z_{2}, ..., z_{K}$}를 각 observation과 연관짓는 동시 발생 데이터에 대한 잠재 변수 모델이다. 즉, PLSA에서는 단어들이 문서에서 마구잡이로 등장하는 것이 아니라, 단어와 문서 사이에 숨겨진 컨셉이 존재한다고 가정한다. 문서가 주어졌을 때, latent concept z를 어떠한 방법으로 추정할 수 있고, 이를 통해 적절한 단어들을 추정할 수 있다는 것이다. 즉, 문서에서 어떤 컨셉, 그리고 해당 컨셉에서부터 단어가 생성되었다는 어떠한 구조를 찾고자 하는 것이다.

예를 들어 그림의 4번째 문서는 TRADE라는 concept에 대해서 작성된 문서이고, trade라는 컨섭에 대해서 다른 단어들보다도 economic, imports, trade라는 단어가 많이 쓰였을 것이라고 추정하고 있다.
PLSA의 모델은 2가지로 볼 수 있는데,

(a) 모델 같은 경우, document가 먼저 생성되고, document로부터 concept이, concept으로부터 term이 생성된다.
(b) 모델 같은 경우, concept이 먼저 정해지고, 그 concept으로부터 document와 term이 각각 생성된다.
D X W에 대한 joint probability model은 다음과 같이 정의할 수 있는데,

해당 모델을 그림으로 나타낸 것이 (a)이다.
이를 다음과 같이 equivalently parameterize 할 수 있다.

이에 대한 그림이 (b)이다.
z의 cardinality가 number of documents, number of words(terms)보다 작기 때문에 z는 단어를 예측하는데에 있어 bottleneck variable과 같은 역할을 한다.
Model Fitting with the EM Algorithm
Likelihood: complete document를 observe할 확률
$L = \prod_{i = 1}^{m}$$\prod_{j=1}^{n}$$p(w_{i}, d_{j})^{n(w_{i}, d_{j})}$
Likelihood가 크면 클수록 모델이 현재의 문서 코퍼스를 생성해낼 확률이 높다.
계산의 편의를 위해 log likelihood function을 만들어주었다.
log likelihood function은 다음과 같다.
$l = \sum_{i=1}^{m}\sum_{j=1}^{n}n(w_{i}, d_{j})log(p(w_{i}, d_{j}))$
$= \sum_{i=1}^{m}\sum_{j=1}^{n}n(w_{i}, d_{j})log(\sum_{l=1}^{k}p(w_{i}|z_{l})p(z_{l})p(d_{j}|z_{l}))$
해당 log likelihood function을 maximize해주는, 혹은 likelihood function을 maximize해주는 closed form solution이 존재하지 않기 때문에, EM(Expectation-Maximization) Algorithm이라는 method를 사용한다. EM 알고리즘은 latant variable을 갖는 모델들의 파라미터를 추정하기 위한 특정 연산을 반복하는 메소드로, 각 반복에서 expectation step과 maximization step을 밟는다.

Expectation Step에서는 $P(z|d, w)$, d라는 document와 w라는 단어가 주어졌을 때, z라는 concept이 얼마만큼 차지하고 있는지에 대한 비율을 계산한다.
* 최초의 $P(w|z), P(d|z), P(z)$ 랜덤하게 initialize된다.
그 후 maximization step에서는
- $P(w|z)$ 즉, w라는 단어가 z라는 concept과 얼마만큼 연관되어있는지를 구한다.
- $P(d|z)$,즉, d라는 문서가 z라는 concept과 얼마만큼 연관되어있는지를 구한다.
- $P(z)$, 즉, 컨셉 z가 얼마나 빈번하게 등장하는지를 구한다.
maximization step에서 새로 얻어진 $P(w|z), P(d|z), P(z)$를 이용하여 다시 expectation step으로 돌아가 $P(z|d, w)$를 update해준다. 그 후, update된 $P(z|d, w)$를 이용해 maximization step에서 3개의 확률을 구한다.
이를 반복하는 것이 EM(Expectation-Maximization) Algorithm이다. EM 알고리즘을 반복적으로 수행하였을 때, 4개의 parameter, $P(z|d, w), P(w|z), P(d|z), P(z)$가 특정한 값으로 수렴할 것이라고 기대한다.
Probabilistic Latent Semantic Space
LSA에서 Term-Document Matrix는 truncated SVD를 통해 $X$ $\approx$ $\hat{X}$ = $TSD'$로 표현되었다.
PLSA도 유사하게 표현이 가능하다. 앞서 언급했던 PLSA에서 $P(d, w)$를 표현하는 방식 중 하나인

를 matrix notation을 이용하여 표현해보자.
$T = (P(d_{i}|z_{k}))_{i, k}), D = (P(w_{j}|z_{k}))_{j, k}), S = diag(P(z_k))_k$로 정의하면, term-document matrix는 LSA에서처럼 $TSD'$로 표현된다. 표현되는 방식은 같지만, PLSA와 LSA는 몇가지 차이점들을 가지고 있다.
PLSA에서는 확률값들을 matrix로 표현한 것이기 때문에, T, D의 모든 값들이 non-negative하고 T에 존재하는 모든 term vector와 D의 모든 document vector들은 합이 1이 된다. 이러한 접근 때문에, LSA에서 k의 값을 수동적으로 구해주어야했던 것과 달리 k의 optimal number도 통계적 방법으로 구할 수 있게 된다.
반면, 단순히 SVD만을 통해 얻어지는 LSA의 구조와는 다르게 특정 연산을 반복적으로 수행하는 EM 알고리즘이라는 기법을 사용하는 PLSA는 계산비용이 더 크다는 우려가 있다. 하지만, 우려와는 달리 저자가 시행해봤던 실험들에서 두 방법의 연산 속도의 큰 차이가 발생하지는 않았고, EM 알고리즘의 연산을 속도를 더욱 높여줄 것이라 생각되는 연구가 가능할 것이라고 본다고 한다.
Topic Decomposition and Polysemy
LSA와 비교했을 때 PLSA는 다의어 문제를 해결하는데에서 우위를 보이는데 이를 아래 예시를 통해 살펴보도록 하자.
아래 표는 1568개의 document를 128개의 latent class(factor, z)를 갖는 PLSA를 통해 학습시킨 후, segment, matrix, line, power라는 단어를 발생시킬 확률이 제일 높은 factor를 단어별로 2개씩 고른 결과라고 한다. 아래 단어들은 $P(w|z)$의 값이 가장 높은 10개의 단어들을 각 factor(z)마다 써놓은 것이다.

SEGMENT, MATRIX, LINE, POWER 모두 첫번째 factor에서와 두번째 factor에서의 의미가 다르다. 즉, 각각의 단어들이 다의성을 가지고 있을 때, 해당 단어의 특정한 의미가 특정 topic에 대해서 각기 다르게 잘 표현이 될 수 있음을 보이고 있다.

실제로도, 문서 1에 segment라는 단어가 주어졌을 때 주제가 $z_{k}$인 확률은 주제가 $z_{1}$일 때가 제일 높고, 문서 2에 segement라는 단어가 주어졌을 때 주제가 $z_{k}$인 확률은 주제가 $z_{2}$일 때가 제일 높다. 반면 특정 문서가 주어졌을 때 segment라는 단어가 등장할 확률이 두 개 문서 모두에 대해 낮은 이유는, 'segment'라는 단어가 등장 자체는 빈번하게 하지만, 모델이 'segment'를 문맥에 따라 다른 의미를 가지는 다의어로 인식하고 있기 때문에 다양한 z에 의해 설명되고 있어 $P(w|z)$가 낮기 때문이고, 따라서 $P(w|d) = \sum_{z}P(w|z)P(z|d)$가 낮은 것이다.
예시
예시를 통해 PLSA에 더욱 친숙해져보자.
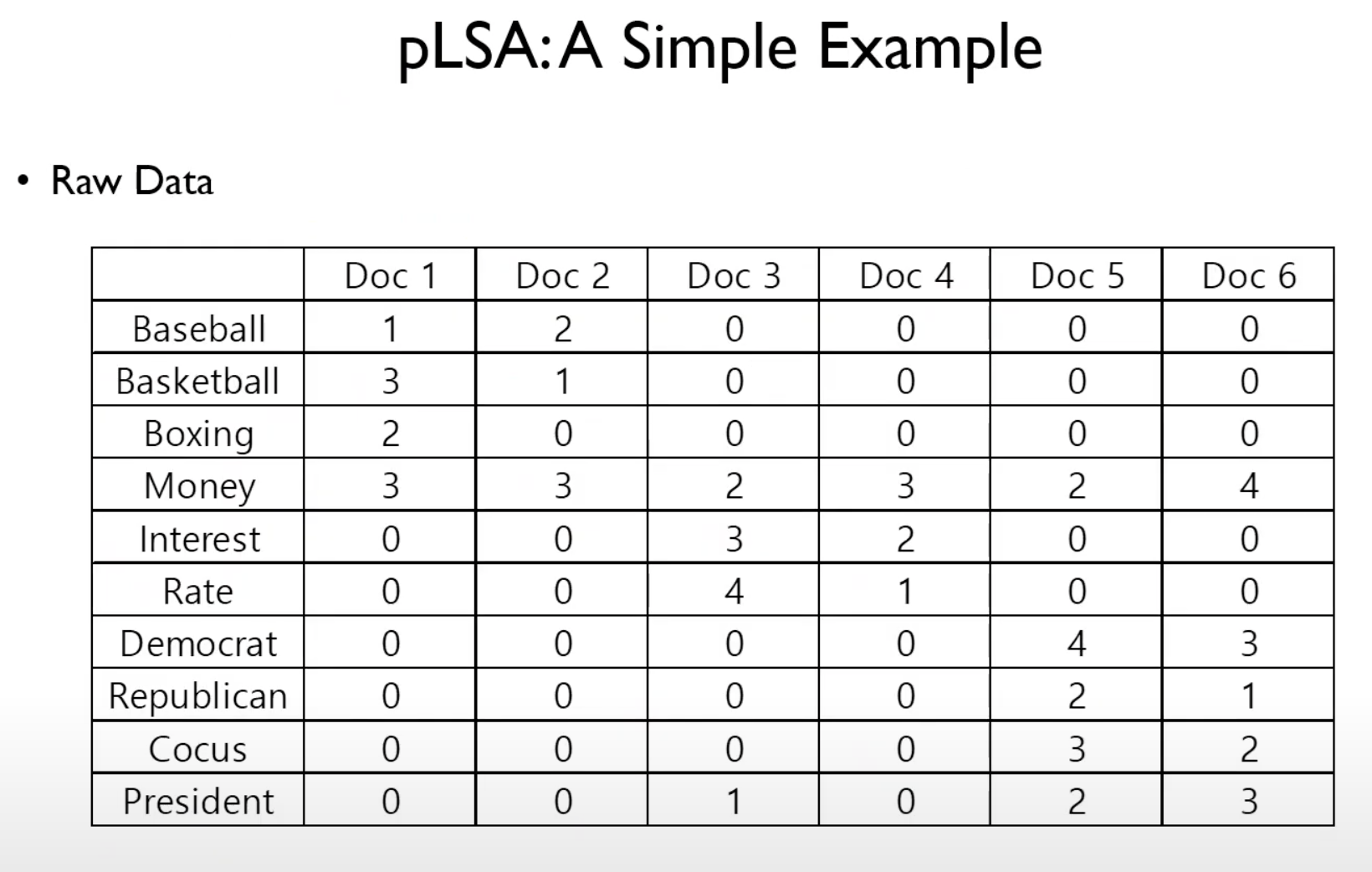
- Baseball, Basketball, Boxing과 같은 단어들이 등장하는 것을 미루어보았을 때, Doc1과 Doc2는 스포츠와 관련된 문서일 것이라고 추정 가능하다.
- Interest, Rate와 같은 단어들이 등장하는 것을 미루어보았을 때, Doc3과 Doc4는 경제와 관련된 문서일 것이라고 추정 가능하다.
- Democrat, Republican, Cocus, President와 같은 단어들이 등장하는 것을 미루어보았을 때, 정치와 관련된 문서일 것이라고 추정 가능하다.
- Money는 스포츠, 경제, 정치 관련 문서에서 모두 등장하고 있다.
우선 $P(w|z), P(d|z), P(z)$를 랜덤하게 initialize한다.
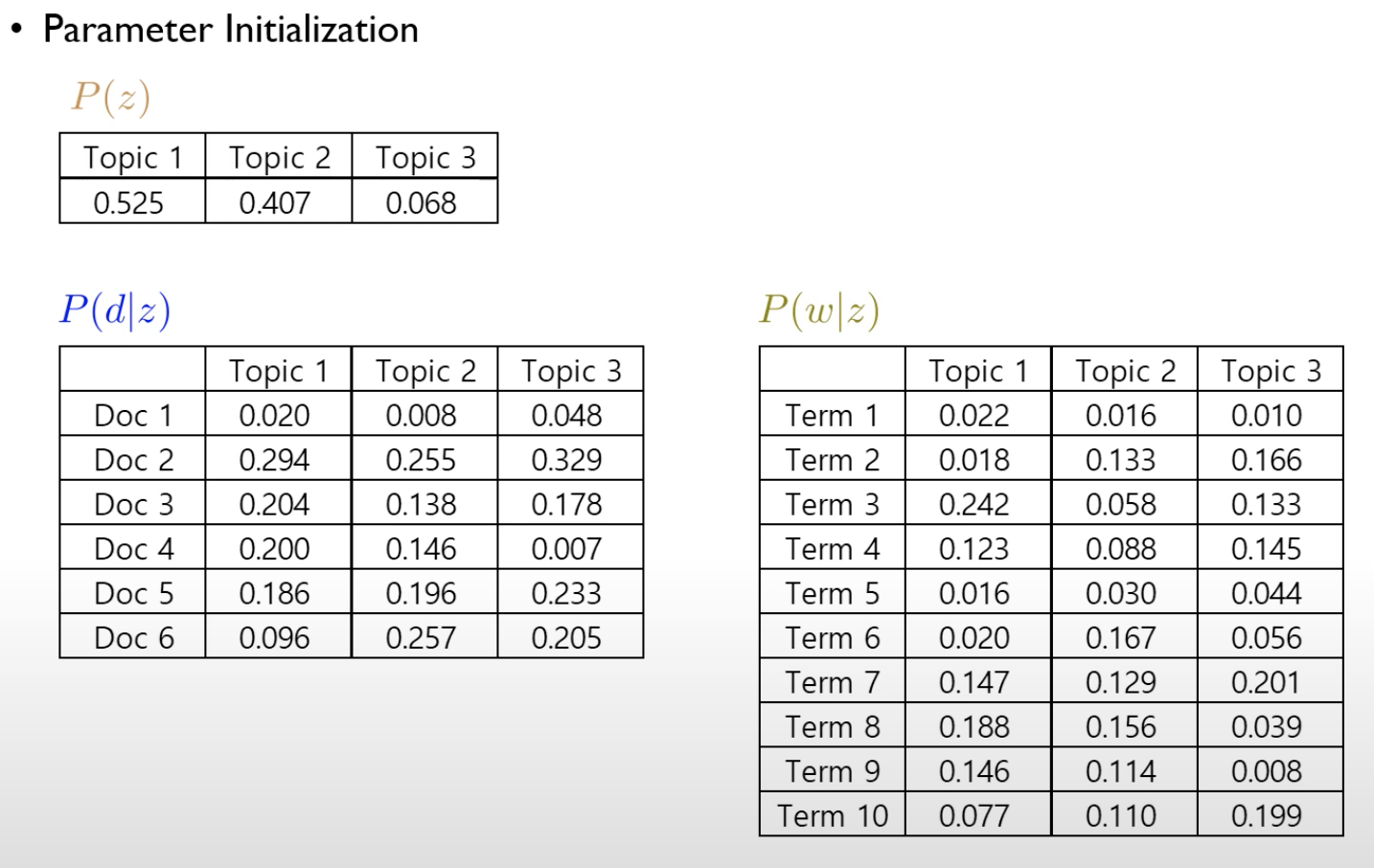
그 후 EM알고리즘을 반복적으로 시행한다.
아래 이미지는 EM알고리즘을 1회 시행한 결과이다.
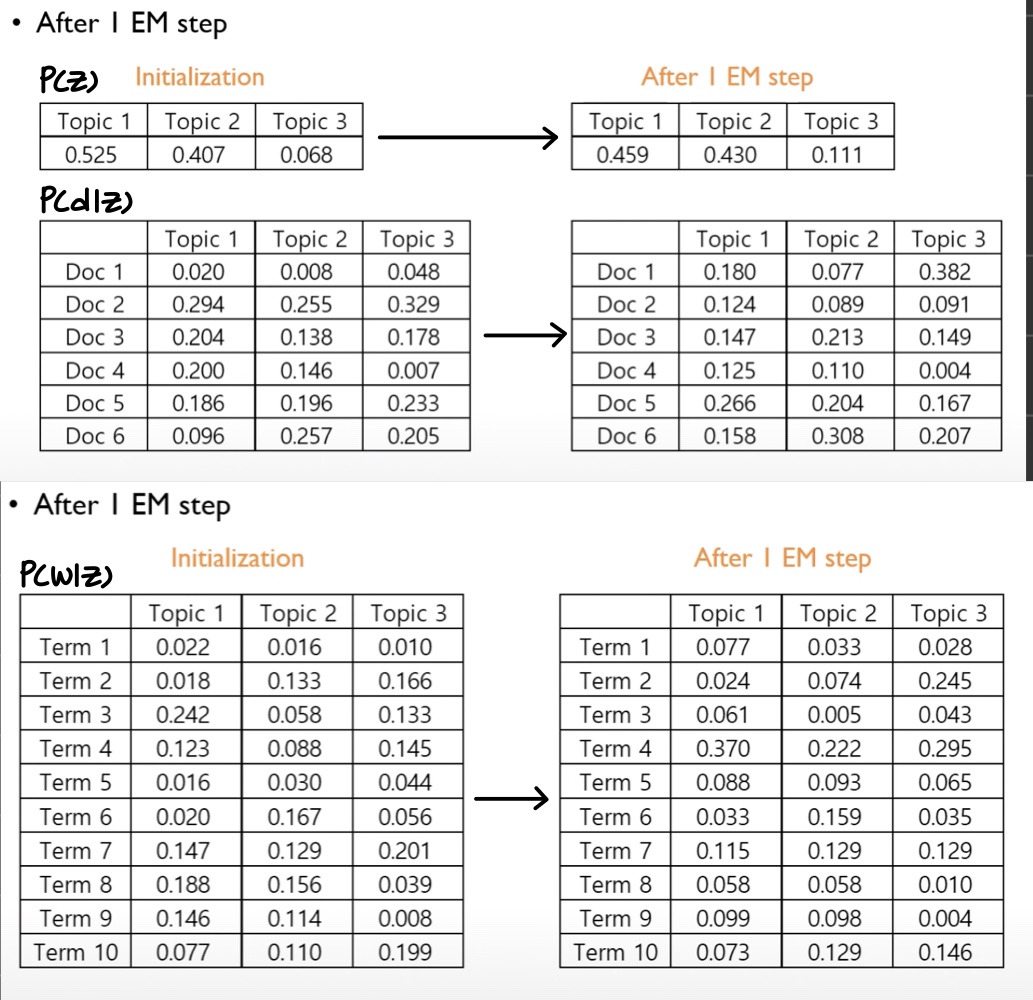
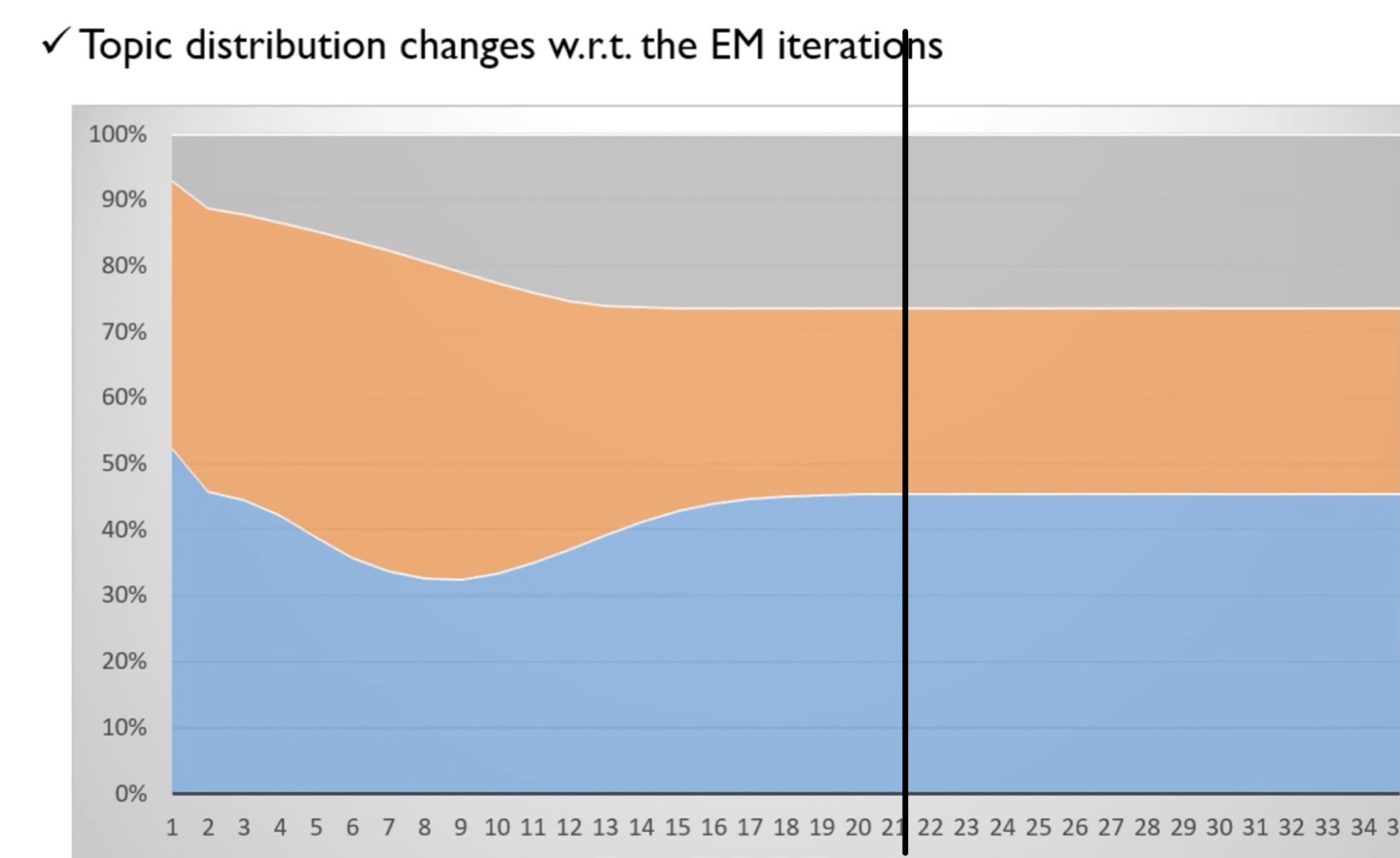
EM알고리즘을 약 20회 정도 반복하였을 때, P(z)의 값이 특정 값으로 수렴하고 있음을 확인할 수 있었다.

최종 결과이다.
Corpus를 통해서 $P(z), P(d|z), P(w|z)$를 추정하였다.
$P(z)$: PLSA를 통해서 추정한 결과, corpus에서 1번 토픽은 45.6%정도를 차지하고 있고, 2번 토픽은 28.1%정도를, 3번 토픽은 26.3%정도를 차지하고 있음을 확인할 수 있다.
$P(d|z)$: 1번 토픽에 대해서 Doc5가 50%, Doc6가 50%를 차지하고 있고, 2번 토픽에 대해서 Doc3이 62.5%, Doc4이 37.5%를 차지하고 있고, 3번 토픽에 대해서는 Doc1이 60%, Doc2가 40% 정도를 차지하고 있다.
$P(w|z)$: 각각의 토픽들에서 각 단어들이 차지하고 있는 비중을 보여주고 있다.
https://www.youtube.com/watch?v=J1ri0EQnUOg&list=PLetSlH8YjIfVzHuSXtG4jAC2zbEAErXWm&index=13
https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/05/25/plsa/
Probabilistic Latent Semantic Analysis · ratsgo's blog
이번 글에서는 말뭉치에 내재해 있는 토픽들을 추론해 내는 확률모델인 Probabilistic Latent Semantic Analysis(pLSA)에 대해 살펴보도록 하겠습니다. 이번 글 역시 고려대 강필성 교수님 강의를 정리했음
ratsgo.github.io
'심화 스터디 > Advanced ML & DL paper review' 카테고리의 다른 글
| [Advanced ML & DL Week2] Neural Ordinary Differential Equations (0) | 2022.09.21 |
|---|---|
| [Advanced ML & DL Week1] ADAM: A Method For Stochastic Optimization (0) | 2022.09.21 |
| [Advanced ML & DL Week2] Faster R-CNN (1) | 2022.09.20 |
| [Advanced ML & DL Week1] Semi-supervised Classification with Graph Convolutional Networks (1) | 2022.09.15 |
| [Advanced ML & DL Week1] World Models (1) | 2022.09.15 |





댓글 영역