고정 헤더 영역
상세 컨텐츠
본문 제목
[Advanced ML & DL Week2] Neural Ordinary Differential Equations
본문
https://arxiv.org/pdf/1806.07366.pdf
제목 : Neural Ordinary Differential Equations
2018 NeurlPS "Best Paper"
저자 : Ricky T. Q. Chen*, Yulia Rubanova*, Jesse Bettencourt*, David Duvenaud
University of Toronto, Vector Institute {rtqichen, rubanova, jessebett, duvenaud}@cs.toronto.edu
업로드일 : [Submitted on 19 Jun 2018 (v1), last revised 14 Dec 2019 (this version, v5)]
Abstract
- 새로운 계열(family)의 심층신경망 모델을 만들었음
- 이산적인 layer 구조에서 벗어나 연속적인 깊이를 가지는 모델임
- 상수 메모리 Cost를 가짐 O(1)
- 연속적인 normalizing flow 모델로도 고안함
- ODE solver를 이용한 backpropagation 방법을 통해 큰 모델을 scalable하게 학습할 수 있음
1 Introduction
Reviewer comment - ResNet의 구조에서 얻을 수 있는 식과 ODE(Ordinary Differential Equations)를 수치적으로 푸는 Euler method의 식이 유사한 것을 이용해 내부 layer를 ODE로 정의하여 solver를 이용한 backpropagation 등을 이용하는 모델입니다.

ResNet, RNN decoders, normalizing flow에서는 다음과 같은 식으로 복잡한 변환들을 표현합니다.

이 식은 Euler discretization(혹은 Euler method)으로 나타낼 수 있습니다.
(Lu et al., 2017; Haber and Ruthotto, 2017; Ruthotto and Haber, 2018)
여기서 더 많은 layer를 추가하고 step을 작게 한다면 결국은 ODE 표현을 통해 연속적인 hidden unit들의 dynamics를 표현할 수 있습니다.
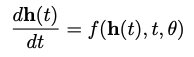
따라서 h(0)부터 시작한다면 어떤 시간 T의 값에 대한 h(T)의 값을 정의할 수 있습니다.
-> black-box 미분방정식 solver로 계산 가능
이외에도 다음과 같은 장점들이 있습니다.
- 메모리 효율성
- 적응적 계산(Adaptive computation)
- 확장가능하고 되돌릴 수 있는 Normalizing flows
- 연속적인 시계열 모델
2 Reverse-mode automatic differentiation of ODE solutions

loss function L()를 최적화하기 위해 ODESolve 과정을 생각해볼 수 있습니다.

L을 최적화하려면 θ에 대한 gradient를 구해야 합니다. 따라서, z(t)의 각 순간에 해당하는 gradient를 구해야 합니다.
이를 adjoint a(t)=∂L/∂z(t)라고 두면 a(t)는 다음과 같은 식을 만족합니다.

이 때 continuous state를 최적화하기 위한 방식은 a(1)에서 시작하여 final state인 a(0)까지 거꾸로 진행되어야 합니다. 이 과정은 ODE를 푸는 과정으로 치환될 수 있습니다.

결과적으로 Algorithm은 다음과 같습니다.

3 Replacing residual networks with ODEs for supervised learning

기존 방법에서는 각 state에서의 모든 gradient를 기억해야 했으나, Adjoint sensitivity method에서는 초기값 a(1)이 주어진 새로운 ODE 과정이고 이후의 state들은 계산을 통해서 구해질 수 있으므로 메모리 효율이 높은 장점이 있습니다.
4 Continuous Normalizing Flows
Normalizing flow (Rezende and Mohamed, 2015)

Planar normalizing flow (Rezende and Mohamed, 2015)

the determinant of the Jacobian ∂f/∂z를 계산하는 것이 큰 병목 지점(O(M^3))이었으나 discrete layers에서 continuous transformation으로 바꾸게 되면 계산 비용을 줄일 수 있습니다.
Theorem 1 (Instantaneous Change of Variables). Let z(t) be a finite continuous random variable with probability p(z(t)) dependent on time. Let dz dt = f(z(t), t) be a differential equation describing a continuous-in-time transformation of z(t). Assuming that f is uniformly Lipschitz continuous in z and continuous in t, then the change in log probability also follows a differential equation,

4.1 Experiments with Continuous Normalizing Flows


5 A generative latent function time-series model

불규칙하게 샘플링된 시계열 데이터에서 ODE를 학습하여 모델을 학습할 수 있고 보간의 형식으로 앞으로의 데이터를 예측할 수 있습니다.


'심화 스터디 > Advanced ML & DL paper review' 카테고리의 다른 글
| [Advanced ML & DL Week2] Sequence to Sequence Learning with Neural Networks (1) | 2022.09.22 |
|---|---|
| [Advanced ML & DL Week2] User Diverse Preference Modeling by MAML (0) | 2022.09.22 |
| [Advanced ML & DL Week1] ADAM: A Method For Stochastic Optimization (0) | 2022.09.21 |
| [Advanced ML & DL Week2] Probabilistic Latent Semantic Analysis (0) | 2022.09.21 |
| [Advanced ML & DL Week2] Faster R-CNN (1) | 2022.09.20 |





댓글 영역