고정 헤더 영역
상세 컨텐츠
본문
작성자: 15기 박지우
1. introduction
ROC(receiver operating characteristics) graph는 분류기의 성능을 파악하여 모델을 고르고 시각화하는데 유용한 기법이다. 시각적으로 맞은 비율과 틀린 비율의 tradeoff를 보여줄 수 있고 보통 진단시스템의 성능을 파악할 때 많이 쓰이는 평가지표이다.

true positive rate = positives correctly classified / total positives (TP/P)
false positive rate = negatives incorrectly classified / total negatives (FP/N)
2. ROC space
: tp rate를 Y축에 넣고 fp rate를 X축에 넣은 이차원 그래프를 ROC 그래프라 한다.
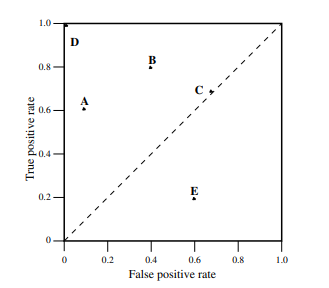
- 점으로 표시된 것을 보았을 때 northwest 방향의 공간에 속해있는 것이 better performance를 보인다고 할 수 있다 . 또 left hand side에 있는 모델은 'conservative'라 표현하는데 positive classification with strong evidence + few false postive errors
- 반대로 upper right hand side에 있는 것은 'liberal'라 표현 -> positive classification with weak evidence + classify nearly all positive correctly + high false positive rates
- 점선으로 표시된 것은 randomly guessing a class -> 점선보다 낮은 위치에 있는 모델은 random guessing보다 좋지 않는 성능을 가지고 있다고 말한다.
3. ranking or scoring classifier
ranking or scoring classifier은 class가 값으로 나오는 것이 아니라 instance마다 확률과 score 수치적 값으로 나온다.
높은 점수가 나오면 높은 확률을 나타내고 이러한 것들을 probabilistic/ classifier라 한다
-> 이 결과값은 적절한 확률로 되지 못한다
그래서 임계값에 따른 binary classifier로 바꿔서 사용할 수 있다
임계값에 따라 ROC graph는 달라지게 된다 -> 임계값을 낮추면 liberal
임계값을 높이면 conservative area로 가는 것을 볼 수 있다

분류기는 정확한 score를 보여줄 필요가 없다.. 그 대신에 positive와 negativve를 구별할 수 있는 상대적 score를 제공 할 수 있으면 된다.

0.5를 임계값으로 했을 때 accuracy metric를 보면 정확도가 80%가 나오는 데 roc curve는 수직과 수평으로 이루어진 것을 볼 수 있다. 즉 perfect performance를 보이고 있다는 것이다.
이 discrepancy(불일치)는 무엇을 측정하고 있는 지를 보고 설명할 수 있다.
ROC curve는 negative instance 대비 postivie instance를 매기기 위해 classifier의 능력을 보여줄 수 있다
accuracy 방법은 score가 적절하다고 하면 사용해도 되지만 score가 적절하지 못하다
ROC curve에서는 기준에 따라 정확성이 달라진다
-> 이 현상을 제거하기 위한 방법은 분류기의 점수를 측정하는 것 & relative performace로 측정하는 것
4. ROC curve의 장점
- class skew
: ROC curve는 class distribution에 변화에 둔감하다는 장점을 가지고 있다. x,y 축을 구성하고 있는 tp rate / fp rate 모두 class distribution에 의존하지 않는 strict ratio이다.

- ROC convex hull
class distribution 또는 error cost와 관련없이 classifier의 성능을 관리하고 시각화할 수 있게 해준다.
-> class skew / error cost 조건에 invariant하다
# iso-perforamce line : slope 'm'에 해당하는 모든 분류기는 같은 expected cost를 가진다
이 라인이 northwest인 것이 더 좋은 것 -> lower expected cost

# convex hull에 있으면 potential optimal이라 할 수 있다
convex hull에 있는 점들은 ROC convex hull (ROCCH)라고 불린다
주의) relative scoring의 결과는 분류기의 점수들은 모델 클래스가 다르다면 비교를 하면 안된다.
왜냐하면 클래스에 따라 score의 범위가 달라지기 때문이다.

5. AUC(Area Under an ROC curve)
: ROC performance를 single scalar value representing expected performance로 바꾸는 것
이 값의 범위는 항상 0-1 사이이다. + random guessing classifier는 0.5의 면적을 가지고 있다
하지만 AUC의 결과를 보고 항상 성능이 좋은 모델이라고 말할 수 없다

6. Averaging ROC curves
ROC curve가 분류기를 평가하기 위해 사용되지만 분류기의 우수성을 결론내리기 위해서는 조금 더 수정이 필요하다
몇몇 연구자들은 그래프만 보고 제일 좋은 모델을 선택한다고 하지만 그것은 한가지 데이터 셋에 대한 정확성만 판단한 것이다
-> variance의 측정없이는 분류기를 비교할 수 없다
-> 다양한 test set을 사용하는 이유는 variance를 측정하기 위해서이다.
그래서 하나의 curve 샘플들을 average하는 averaging ROC curve 방법을 사용하는 것이다
1) Vertical averaging

FP rates fixed 하고 그에 대응하는 TP rate의 평균을 내는 방법이다
함수로 표현 하면 R_hat(tp_rate) = mean[R_i(fp_rate)]
2) Threshold averaging

위의 방법의 한계는 true positive rate만 변수로 놓는다는 점이다
그래서 다른 독립변수를 false positive rate으로도 두는 것이다
각 포인트마다의 threshold에 따라 계산이 되어진다.
샘플마다의 threshold를 생성해서 그에 맞는 ROC 포인트와 평균을 내는 것
이것도 하나의 단점을 가지고 있는 데 임계값평균방법을 사용하려면 분류기의 점수를 각 포인트마다 필요하다 + 클래스가 다르면 비교가 어렵다는 단점
7. Interpolating classifier
때때로 특정 분류기가 원하는 퍼포먼스를 나타내지 않을 때가 있다
요구하는 퍼포먼스를 가져오기 위해서 샘플링하는 방법이 있다.
-> 만약 두개의 분류기를 샘플링 했는데 두 분류기의 중간 수준의 퍼포먼스를 가지는 분류기를 가져오고 싶다
그 때의 방법은 선형 interpolation을 통해서 K값을 구해서 그 분류기의 퍼포먼스를 구할 수 있다.
만약 K 0.53이라 하면 B의 결정을 0.53비율로 뽑고 A의 결정을 0.43비율로 뽑는 것이다.
-> 원하고자 하는 C의 퍼포먼스가 나온다






댓글 영역