고정 헤더 영역
상세 컨텐츠
본문
* 작성자 : 15기 최민경
본 포스팅은 Youtube 김성범 교수님의 ARIMA 모델 - Part6 강의를 참고하여 작성되었습니다.
<복습>
Q1. AR모델도 white noise의 linear combination으로 표현이 가능하다. (O/X)
A. O
Q2. ARMA모델도 white noise의 linear combination으로 표현이 가능하다. (O/X)
A. O
Q3. white noise인 $a_t$의 성질은?
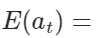
0
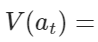
$\sigma _{a}^{2}$

0, 시점이 다른 확률변수는 서로 독립
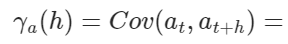
$\sigma _{a}^{2}$ $h=0$일 때
0 $h \neq 0$일 때
Prediction(Forecasting)
Given $x_1, x_2, \cdots , x_t$, want to predict $x_{t+1}$
min $ E[(x_{t+1}-\hat{x}_{t+1})^2]$
-> MSE 최소화하는 $\hat{x}_{t+1}$ 찾기
즉, $\hat{x}_{t+1} = E[x_{t+1}|x_1, \cdots x_t]$
-> conditional expectation
1. AR(1)

Q. 여기서 $\mu$의 역할은?
A. constant term
Q. 그렇다면 $\hat{x}_{t+1}$는 어떻게 표현될까?
A. $x_{t+1}$의 conditional expectation으로
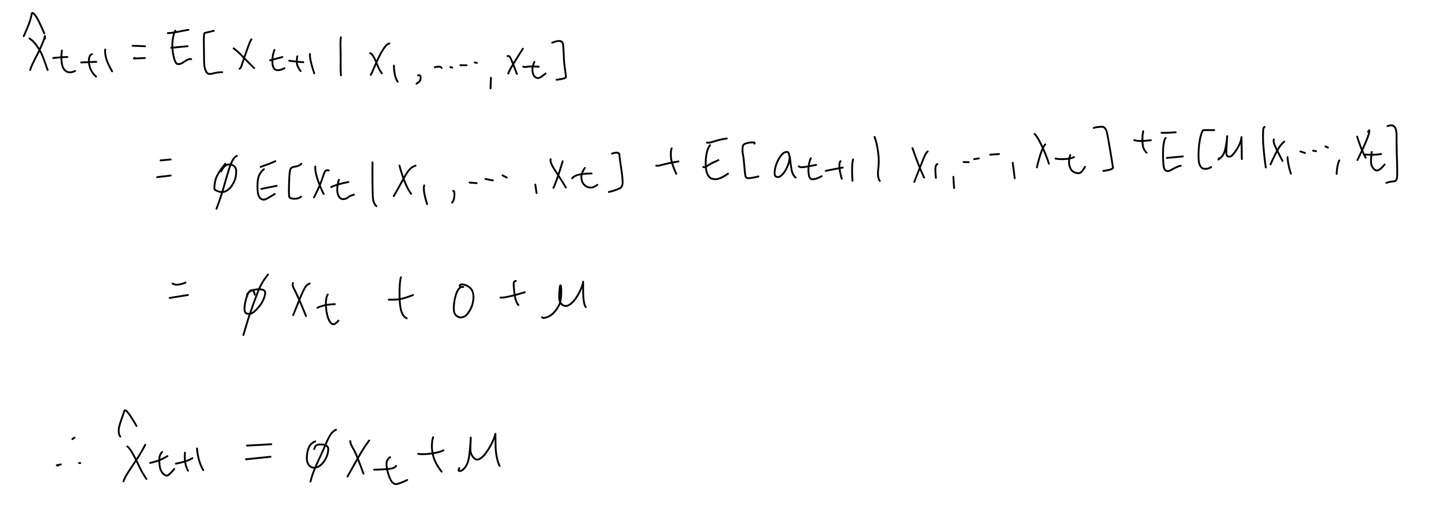
-> 점추정(point estimation)
prediction interval
Q. prediction interval과 confidence interval의 차이점은 무엇일까?
A. confidence interval은 population의 mean값의 confidence를 주는 것이고, prediction interval은 모델에 대해 새로운 데이터가 가지게 될 예측값의 confidence를 주는 것. Prediction interval은 mean값과 달리 point값을 예측하는 것이기 때문에 큰 uncertainty를 포함하고 있어 confidence interval에 비해 interval이 더 넓게 나타난다.
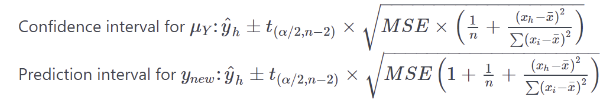

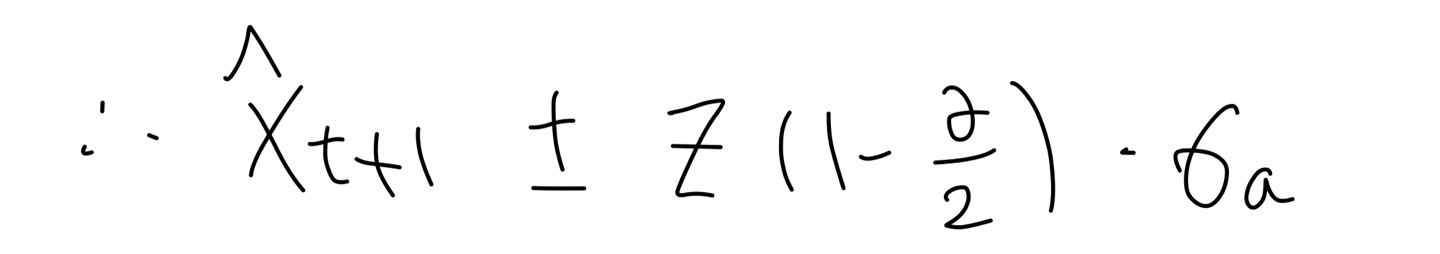
정리해보면,
AR(1) model's point estimation = $\hat{x}_{t+1}=\phi x_t+\mu$
$\hat{x}_{t+2}=\phi x_{t+1}+\mu$
prediction interval = $\hat{x}_{t+1} \pm z(1-\frac{\alpha}{2})\cdot \sigma _{a}$
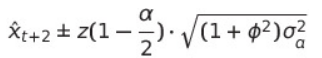
2. AR(2)
- point predicted value : $\hat{x}_{t+1} = \mu +\phi _{1} x_t + \phi _{2} x_{t-1}$
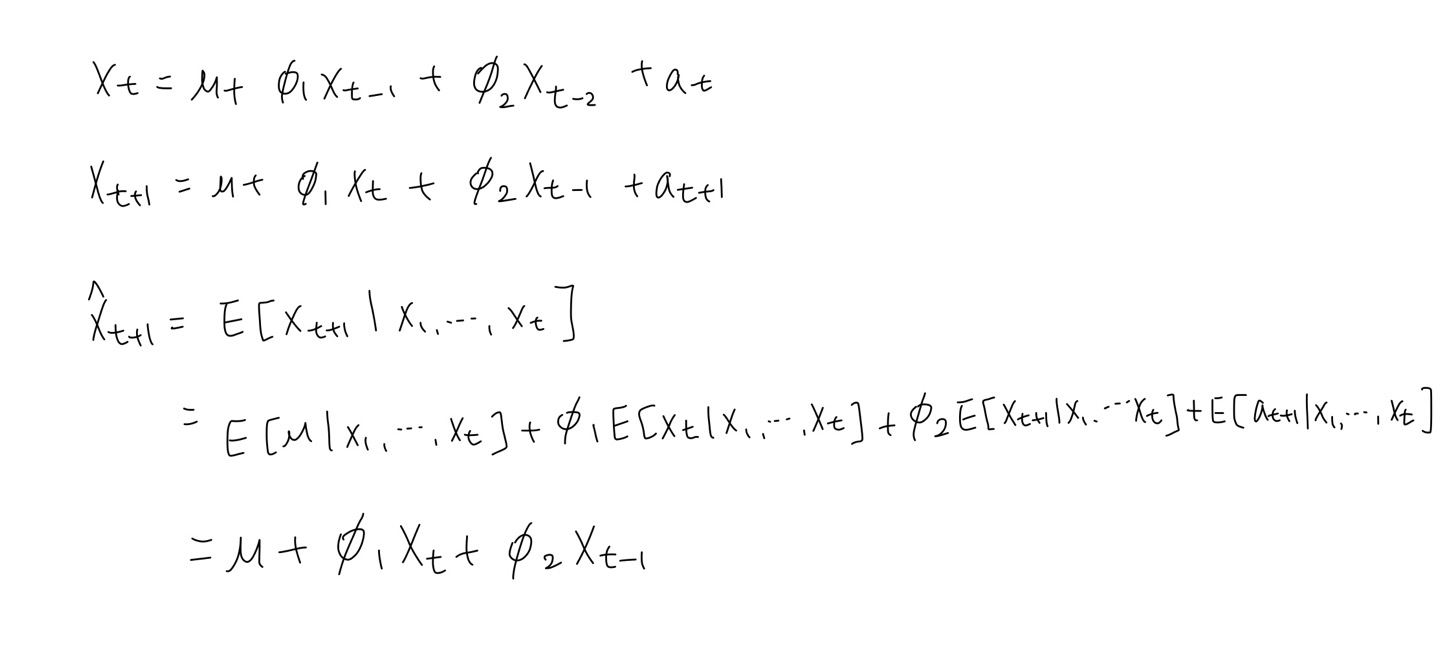
- prediction interval :
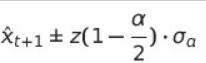
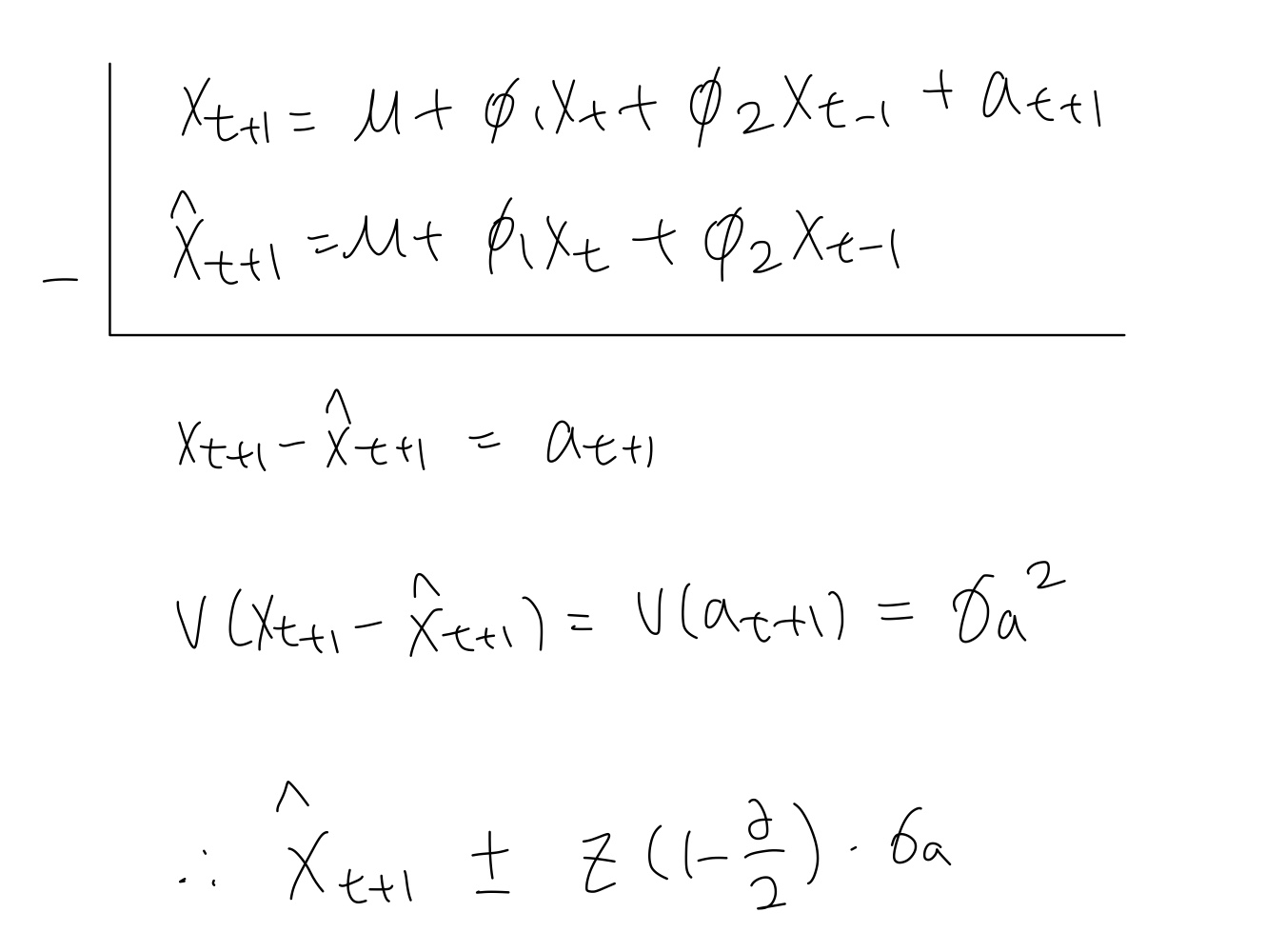
- point predicted value : $\hat{x}_{t+2}=\mu +\phi_{1} \hat{x}_{t+1} + \phi_{2} x_{t}$
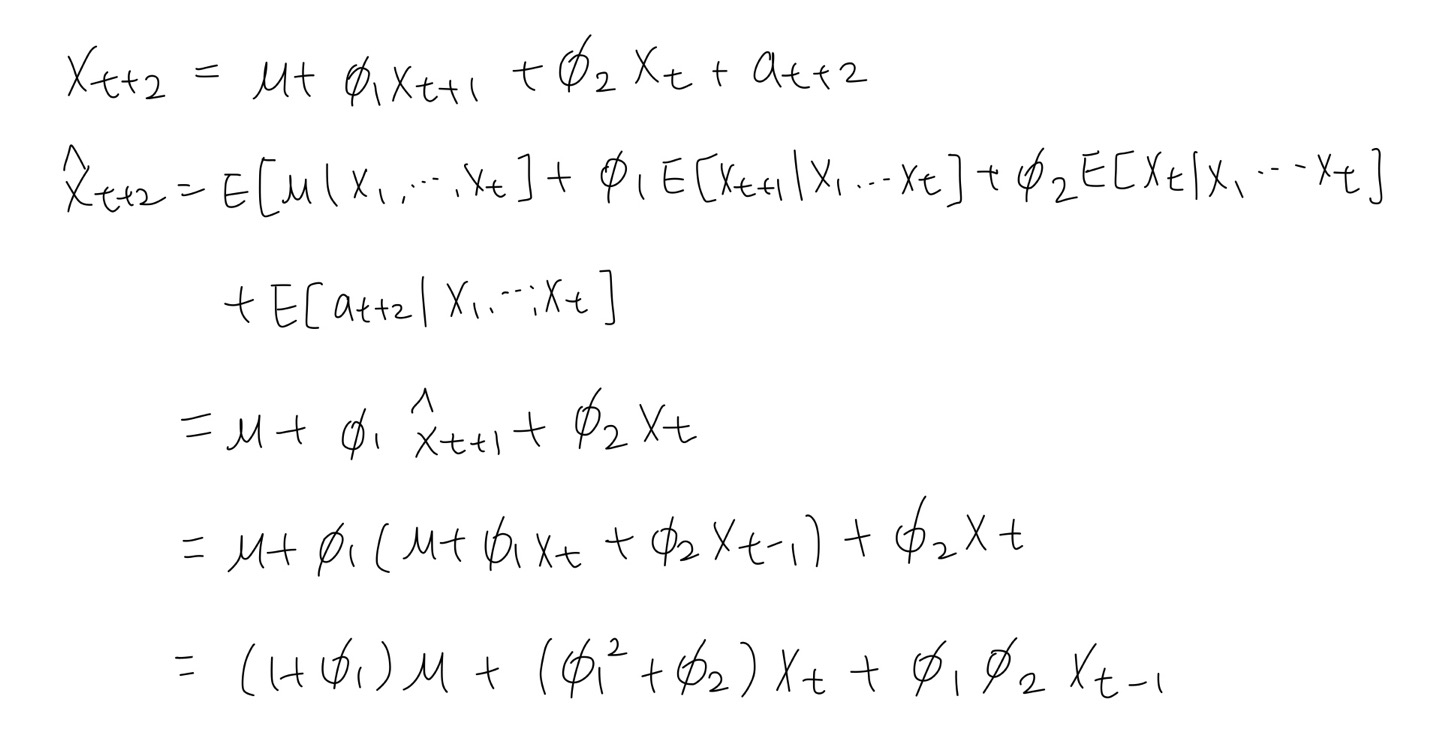
- prediction interval : $\hat{x}_{t+2}\pm z(1-\frac{\alpha}{2})\cdot\sqrt{(1+\phi_{1} ^2)\sigma_{a}^2}$

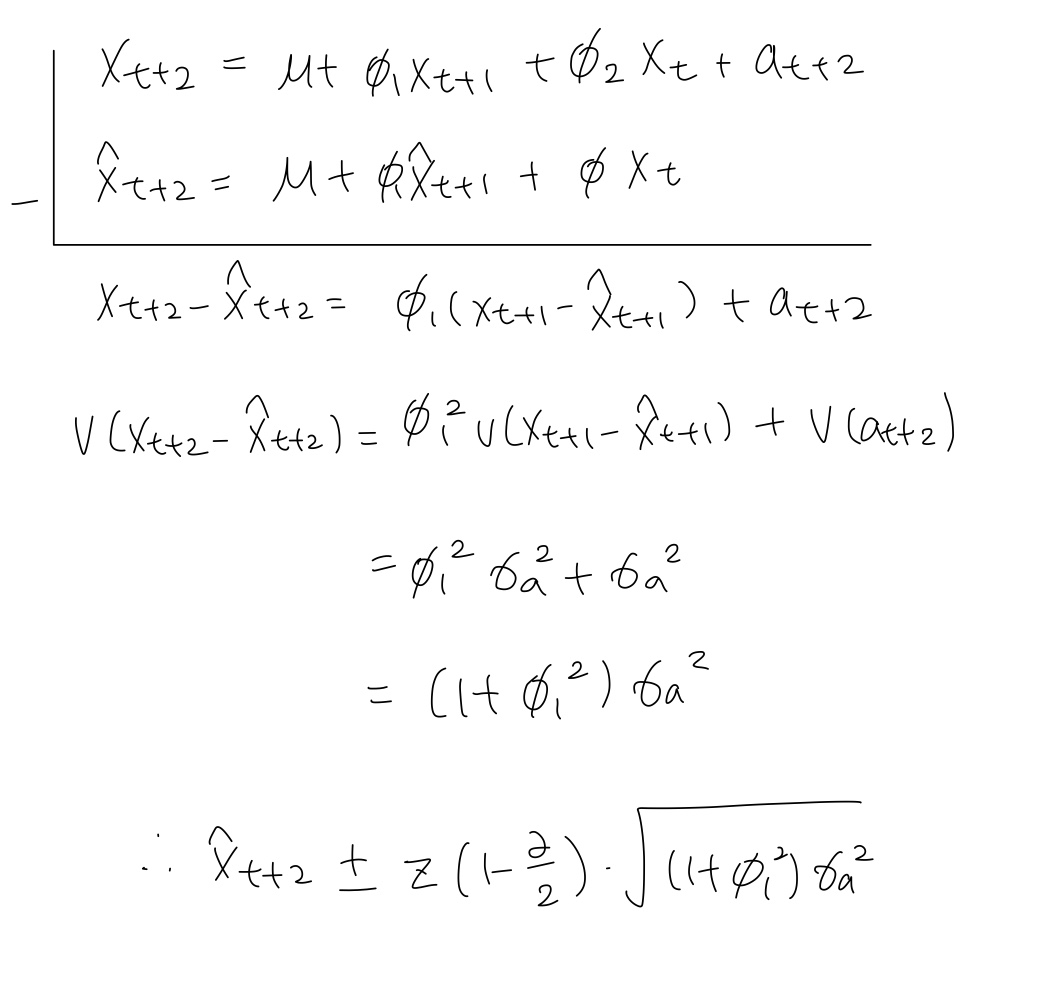
- point predicted value : $\hat{x}_{t+3}=\mu +\phi_{1} \hat{x}_{t+2} + \phi_{2} \hat{x}_{t+1}$

- prediction interval : $\hat{x}_{t+3}\pm z(1-\frac{\alpha}{2})\cdot \sqrt{(1+\phi_{1}^2(1+\phi_{1}^2)+\phi_{2}^2)\sigma _{a}^2}$
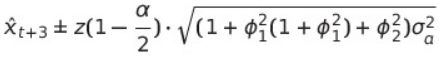
3. ARMA(1,1)
- point predicted value : $\hat{x}_{t+1} = \phi x_{t} + \theta \tilde{a_{t}} +\mu$
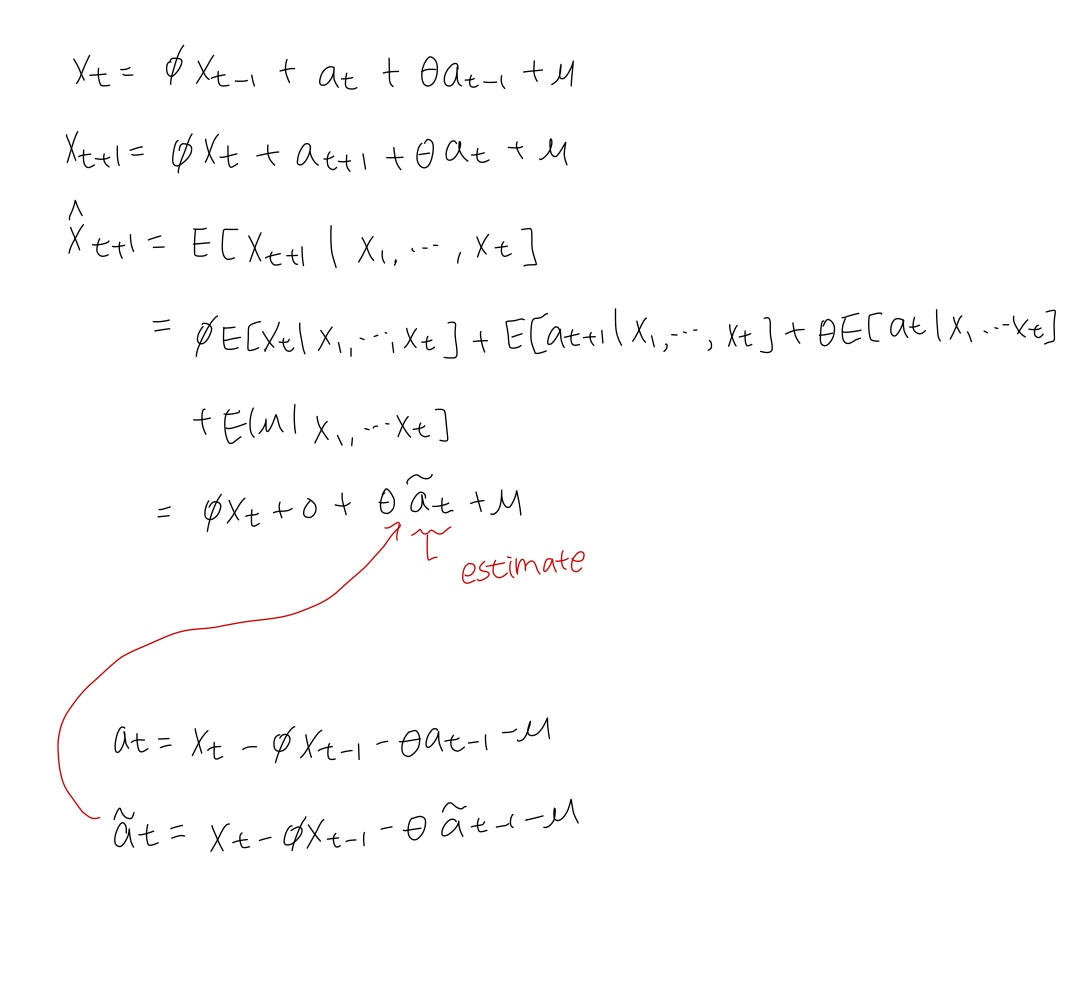
Q. ARMA(1,1)은 위에서 주어진

말고 다르게 표현할 수 있는데, 과연 어떻게 표현할 수 있을까?
A. white noise의 무한합으로 표현 가능
- prediction interval : $$\hat{x}_{t+1} \pm z(1-\frac{\alpha}{2})\cdot \sigma_{a}$$
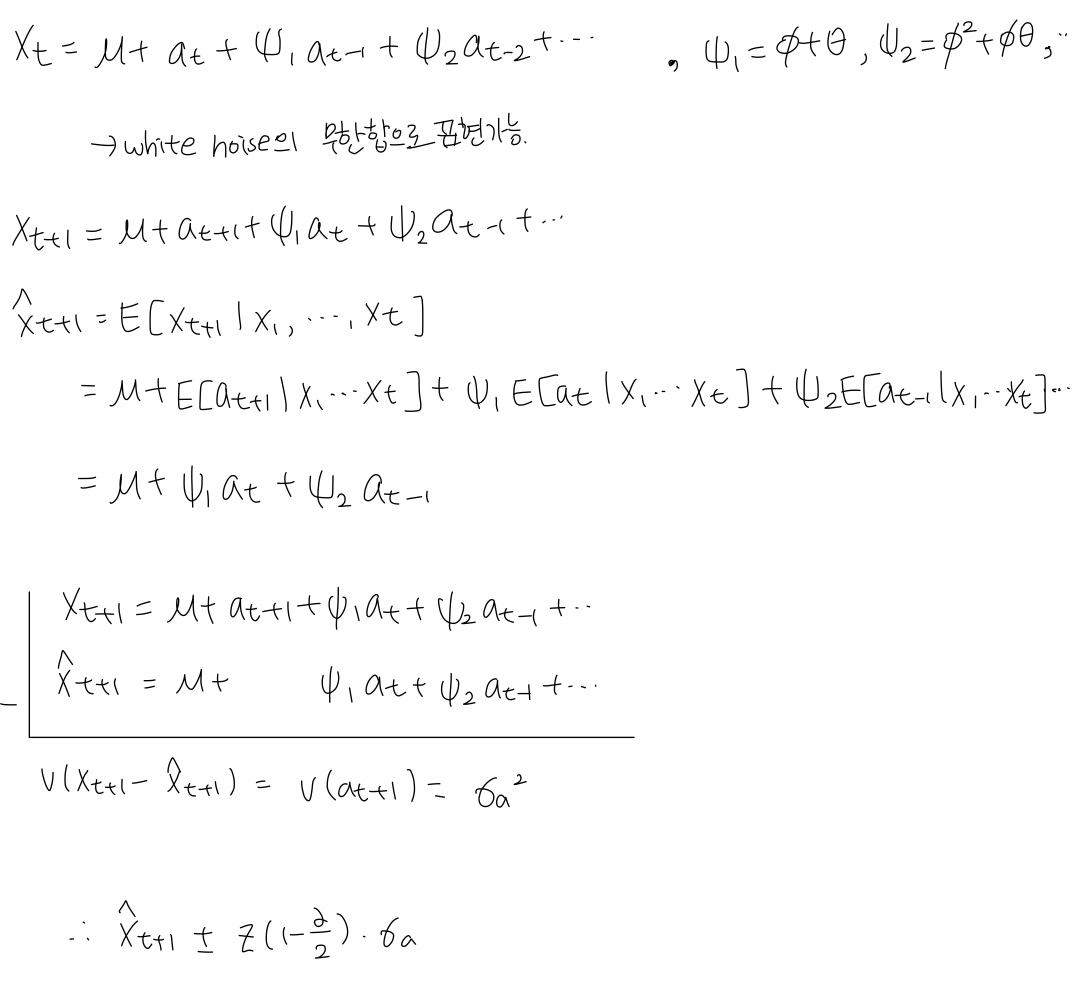
Q. 위와 같이 $x_{t+1}$의 PI를 구할 수 있는데, 그렇다면 $x_{t+2}$의 PI는 길이가 어떻게 될까?
A. 더 길어진다. 더 먼 미래를 예측하는 것이기 때문에 더 긴 구간으로 예측한다.
- (1-a)100% Prediction Interval for $x_{t+2}$ in ARMA(1,1)
= $\hat{x}_{t+2} \pm z(1-\frac{\alpha}{2})\cdot \sqrt{(1+\psi_{1} ^2)\sigma _{a}^2}, \psi_{1}=\psi +\theta$
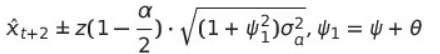
- (1-a)100% Prediction Interval for $x_{t+3}$ in ARMA(1,1)
= $\hat{x}_{t+3} \pm z(1-\frac{\alpha}{2})\cdot \sqrt{(1+\psi_{1} ^2+\psi_{2} ^2)\sigma _{a}^2}, \psi_{1}=\phi +\theta, \psi_{2}=\phi^2 +\phi\cdot\theta$

4. PACF(Partial autocorrelation function)

ACF에서 시차 사이에 낀 다른 시차의 영향력을 제거한 함수
- conditional function
- correlation between two variables under the assumption that we take into account the values of some other set of variables.
The partial correlation between Y and $X_3= \frac{Cov(Y,X_3|X_1, X_2)}{\sqrt{V(Y|X_1, X_2)\cdot V(X_3|X_1, X_2)}}$
The partial correlation between $X_{t} and X_{t-h}$
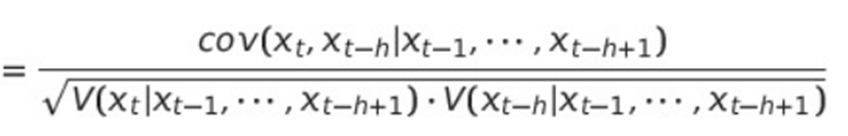
$X_{t-h}=\frac{cov(x_t, x_{t-h}|x_{t-1},\cdots,x_{t-h+1})}{\sqrt{V(x_t|x_{t-1},\cdots,x_{t-h+1})\cdot V(x_{t-h}|x_{t-1},\cdots,x_{t-h+1})}}$
'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열 스터디] 코드리뷰(1) (0) | 2022.11.24 |
|---|---|
| [시계열 스터디] ARIMA 모델 part5 (0) | 2022.11.13 |
| [시계열] ARIMA 모델 - Part 4 (0) | 2022.11.03 |
| [시계열 스터디] ARIMA Model part3 (0) | 2022.10.09 |
| [시계열 스터디] ARIMA Model part2 (1) | 2022.09.25 |





댓글 영역