고정 헤더 영역
상세 컨텐츠
본문

| 해당 게시글은 고려대학교 김성범 교수님의 ARMA 모델 - Part 5 영상을 기반으로 작성되었습니다 |
통합 + 심층 자문자답 Review
ARIMA 모델은 정상성(Stationary)을 이미 가졌을 때에 사용
정상성(Stationary)
1. 평균이 모든 시점 t에서 동일하다 : 추세, 계절성, 순환성 등의 패턴이 더이상 존재하지 않는다.
2. 분산이 모든 시점 t에서 동일하다 : 자료 변화의 폭이 일정하다
의문 1)
stationary의 정의는 추세, 계절성, 순환성 등의 패턴이 더이상 존재하지 않는 경우라고 한다.
내가 생각하기에 시계열 데이터를 굳이 분석하는 이유는 그 데이터 속에 숨겨져 있는 '시계열'이 궁금해서이지 않은가?
즉, 그 데이터가 어떤 추세를 가지는지, 어떤 계절성을 가지는지를 알아내는 것이 핵심이라고 생각되는데 데이터가 차분을 통해 stationary하게 되었다면, 그 데이터는 이제 평범한 데이터 아닌가?
추세, 계절성, 순환성이 보이지 않는 데이터를 왜 시계열 모델을 통해 분석하는 것인가?
이미 stationary해진 데이터에서 왜 독특한 형태의 ACF와 PACF가 생겨나는 것이고 stationary한 이후에도 그 데이터가 시계열 데이터인 이유는 무엇인가?
해답)
차분은 데이터를 stationary하게 만들어준다고 하지만 정확하게는 weak stationary(약 정상성)하게 만들어주는 과정이다
※약 정상성은 기존 정상성을 만족하지만 공분산값은 시간 t에 의존하지 않고 오직 시차 (k)에만 의존하는 경우
결국 차분은 데이터의 전체적인 형태를 변환시킬 뿐, 시차의 영역은 보정해주지 않는다
(엄격한 의미의 강 정상성은 시차에 따라서도 공분산값이 일정함)
MA모델, AR모델, ARMA모델
ARIMA는 기본적으로 인자를 p,d,q를 갖는다. 이 때, p는 자기회귀의 차수, d는 차분의 횟수, q는 이동평균의 차수(과거 몇 개의 데이터를 사용할지)를 의미한다.(단, p,q는 보통 차수2를 넘지 않는다.)
AR모델(Auto Regressive Model)

여기서 p의 값은 무슨 의미?
우리의 '데이터'는 서로 연속되는 p개의 데이터들끼리 서로 연관을 가지고
p+1개 이상의 시차를 가질 경우 서로 연관이 없다
MA모델(Moving Average Model)

여기서 q의 값은 무슨 의미?
우리의 '데이터 속 error값'은 서로 연속되는 q개의 데이터들끼리 서로 연관을 가지고
q+1개 이상의 시차를 가질 경우 서로 연관이 없다
ACF와 PACF에 따른 모델 hyperparameter 선택

그렇다면 ACF와 PACF를 알아보자
자기 공분산 함수(AutoCovariance function)

ACF(AutoCorrelation Function) : 자기상관 함수

※stationary하기 때문에 분산은 시점에 상관없이 같은 값
PACF(Partial ACF) : 편자기상관 함수

※두 수식을 비교하며 쳐다보면 PCAF는 ACF에다가 조건부확률을 통해 두 항을 제외한 나머지 항들의 영향력을 제거해 주었다. 나머지 항들의 영향력을 제거한다는 것이 의미적으로 쉽게 와닿지 않는데 그 조건이 있고 없고는 각각의 값에 어떤 차이를 불러일으킬까?


말그대로 error term끼리의 상관관계를 구한다고 보면 된다
의문 2)
ACF값이 뚝 떨어지는 이유는 PART4에서 수식적으로 증명하였다.
그렇다면 AR모델과 MA모델이 가지는 정의와 ACF, PACF를 연관지어 어떻게 설명할 수 있을까?
AR모델은 왜 ACF가 아닌 PACF가 cut off 되는 것이고 MA모델은 왜 PACF가 아닌 ACF가 cut off 되는 것일까
ACF가 0이면서 PACF가 0이 아닌 경우는 무슨 뜻이고, PACF가 0이면서 ACF가 0이 아닌 경우는 무슨 뜻일까
그리고 ACF와 PACF가 각각 0이 되는 것과 그 시점이 p, q인 이유는 무엇일까?
해답)
AR모델과 MA모델을 각각 나누어 생각해보자
'AR 모델의 Hyperparameter p가 2이다' 라는 문장은 어떤 의미일까?
-> 우리의 데이터 Yt는 yt, y(t-1), y(t-2) 3개의 연속된 데이터끼리만 서로 영향을 미친다고 생각한다
그렇다면 yt와 y(t-3)은 독립인가? 정답부터 말하자면 NO
좀 더 깊이있게,
AR모델을 간단하게 yt = a + b·y(t-1)이라고 해보자(a,b는 모두 1보다 작다)
이 때, y(t-1) = a + b·y(t-2)이기 때문에 대입해보면
yt = a + b·(a + b·y(t-2)) = a + ab + b^2·y(t-2)로 풀어낼 수 있다
이런 식으로 전개한다면 AR 모델은 과거의 어떤 데이터이든지 b^h (h는 시차)만큼의 연관성을 가지고 있다.
이것이 AR 모델의 ACF 값이 0으로 떨어지지 않는 이유이다.
AR모델의 시점 p=2라는 뜻은 결국 시차가 3 차이나는 데이터와 현재 데이터가 독립이라는 뜻이 아니라 AR 모델에 들어있는 그 전 데이터들에 의해 변환되었을 때에만 영향을 미친다는 뜻이다.
결국 PACF가 조건부 확률로써 중간 데이터들의 영향력을 제거한다는 의미를 언어로 풀어내자면

이 과정을 통해
yt 수식에 존재하는 y(t-1)에다가 다시 y(t-1)에 존재하는 y(t-2)를 넣을 수 없도록 중간다리를 끊는다고 받아들이면 된다.
AR 모델에서의 error는 i.i.d 하기 때문에
y(t-p)가 더이상 yt에 존재하지 않게 되는 순간 PCAF는 정확히 0이된다
그렇기에 AR모델은 ACF가 0이 되지 않으면서 동시에 PACF는 0이 되는 것이다
이 개념을 그대로 이해하면 MA 모델에 적용하는 건 비교적 수월하다
MA 모델을 간단하게 yt = et + a·e(t-1)이라고 해보자 AR과 다른 점은 시점 t를 설명하기 위해서 가져오는 과거의 t-1 시점의 데이터는 y(t-1)아니다 그 말인 즉슨 AR 모델에서는 y(t-1), y(t-2) ..... y(t-100) 모든 과거의 시점을 대입만 하면 가져올 수 있지만 MA 모델에서는 과거 시점의 et를 잠시 가져왔다가 시점이 변하면 그 e는 작아지는 형태가 아니라 사라지는 형태이다.
따라서 MA 모델의 ACF는 시점 q가 지나면 완벽히 0으로 떨어지게 된다.
MA 모델에서는 yt와 y(t-2)가 진짜 독립이다!
PACF는 et와 e(t-h) 사이의 correlation이라는 것만 이해한다면 AR 모델과 같은 논리로 이해할 수 있다.
PACF는 error term 사이의 상관관계를 의미한다
MA 모델에서의 error는? AR 모델에서의 yt와 정확하게 똑같이 움직인다 따라서 똑같은 논리회로를 거쳐 MA 모델에서는 a^h (h는 시차) 만큼 데이터의 error는 시차 h 이전의 error와 연관되어 있다
이것이 MA 모델의 PACF 값이 0으로 떨어지지 않는 이유이다
part 4 간단 정리
AR모델, MA 모델의 ACF Function 유도
part 5 강의 내용
1. ARMA 모델의 ACF를 구해보자
2. ARMA모델을 white noise에 linear한 연산으로 표현해보자
Backward shift operator
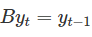
yt에 붙어 yt를 y(t-1)로 밀어주는 연산자
+)다음과 같이 differencing을 설명해줄 수 있는 연산자



ARIMA 모델에 활용

Autocovariance function of ARMA(1,1) h=0

Autocovariance function of ARMA(1,1) h=1


Autocovariance function of ARMA(1,1) h>=2

Autocorrelation은 Autocovariance를 scaling해 준 값이므로 Autocovariance function의 모습을 통해 ACF를 유추할 수 있다
AR(p)


white noise (at)는 특정한 function을 거치면 AR(p)모델이 된다
MA(q)


ARMA(p,q)

결론
AR, MA, ARMA 모델은 white noise가 linear한 function을 거쳐 생성된 형태로 표현할 수 있다
'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열 스터디] ARIMA Code Reading (0) | 2022.11.25 |
|---|---|
| [시계열 스터디] 코드리뷰(1) (0) | 2022.11.24 |
| [시계열 스터디] ARIMA Model part6 (1) | 2022.11.13 |
| [시계열] ARIMA 모델 - Part 4 (0) | 2022.11.03 |
| [시계열 스터디] ARIMA Model part3 (0) | 2022.10.09 |





댓글 영역