고정 헤더 영역
상세 컨텐츠
본문

작성자: 고태영
본 코드리뷰는 https://www.kaggle.com/code/kanncaa1/time-series-prediction-tutorial-with-eda/notebook을 참고하여 작성하였습니다.
관련 라이브러리 및 데이터 불러오기 / EDA의 경우 생략
(1) 데이터 Cleaning
# drop countries that are NaN
aerial = aerial[pd.isna(aerial.Country)==False]
# drop if target longitude is NaN
aerial = aerial[pd.isna(aerial['Target Longitude'])==False]
# Drop if takeoff longitude is NaN
aerial = aerial[pd.isna(aerial['Takeoff Longitude'])==False]
# drop unused features
drop_list = ['Mission ID','Unit ID','Target ID','Altitude (Hundreds of Feet)','Airborne Aircraft',
'Attacking Aircraft', 'Bombing Aircraft', 'Aircraft Returned',
'Aircraft Failed', 'Aircraft Damaged', 'Aircraft Lost',
'High Explosives', 'High Explosives Type','Mission Type',
'High Explosives Weight (Pounds)', 'High Explosives Weight (Tons)',
'Incendiary Devices', 'Incendiary Devices Type',
'Incendiary Devices Weight (Pounds)',
'Incendiary Devices Weight (Tons)', 'Fragmentation Devices',
'Fragmentation Devices Type', 'Fragmentation Devices Weight (Pounds)',
'Fragmentation Devices Weight (Tons)', 'Total Weight (Pounds)',
'Total Weight (Tons)', 'Time Over Target', 'Bomb Damage Assessment','Source ID']
aerial.drop(drop_list, axis=1,inplace = True)
aerial = aerial[ aerial.iloc[:,8]!="4248"] # drop this takeoff latitude
aerial = aerial[ aerial.iloc[:,9]!=1355] # drop this takeoff longitude
NaN 값 제거 및 필요없는 변수를 제거한다.
(2) 최종 데이터
weather_station_id = weather_station_location[weather_station_location.NAME == "BINDUKURI"].WBAN
weather_bin = weather[weather.STA == 32907]
weather_bin["Date"] = pd.to_datetime(weather_bin["Date"]) #datetime 형식으로 바꿔줌
plt.figure(figsize=(22,10))
plt.plot(weather_bin.Date,weather_bin.MeanTemp)
plt.title("Mean Temperature of Bindukuri Area")
plt.xlabel("Date")
plt.ylabel("Mean Temperature")
plt.show()세계 2차대전 관련 BINDUKURI 지역에 대한 일단위 평균 온도(1943년 5월 11일~1945 5월 31일)
총 751개의 데이터

시각화

Q1. 다음 데이터에 정상성이 있다고 할 수 있을까? (x)
Q2. WHY?
(seasonal variation이 있음을 유추할 수 있다. 여름에는 평균온도가 높고 겨울에는 평균온도가 낮은 패턴을 보인다.)
(3) 정상성 Review
Q3. Arima 모델은 (정상성)을 가정한다.
Q4. 정상성?
A. (평균)과 (분산)이 시간에 따라 일정한 성질
Q5. 정상성을 찾아보자

(b),(g) = (정상성 만족)
(d),(h) = seasonal variation이 보여서 정상성 만족x
(a),(c),(e),(f) = (특정한 trend가 있어서 정상성 만족x)
(i) = seasonal variation+trend+시간에 따라 분산이 커져서 정상성 만족x
(4) 정상성 파악하기
1. 위와 같이 Raw 그래프의 패턴을 보고 정상성 유추
2. ACF(Auto Correlation Function) 그래프

Q6. 다음 ACF 그래프에서 정상성을 가지는 그래프는? (3번)
ACF 그래프가 급격히 감소하거나 일정한 패턴이 없는 경우 -> stationary
ACF 그래프가 천천히 감소하는 경우 -> nonstationary
#데이터에 적용해보기
import statsmodels.api as sm
fig=plt.figure(figsize=(20,8))
ax1=fig.add_subplot(211)
fig=sm.graphics.tsa.plot_acf(ts, lags=20, ax=ax1)
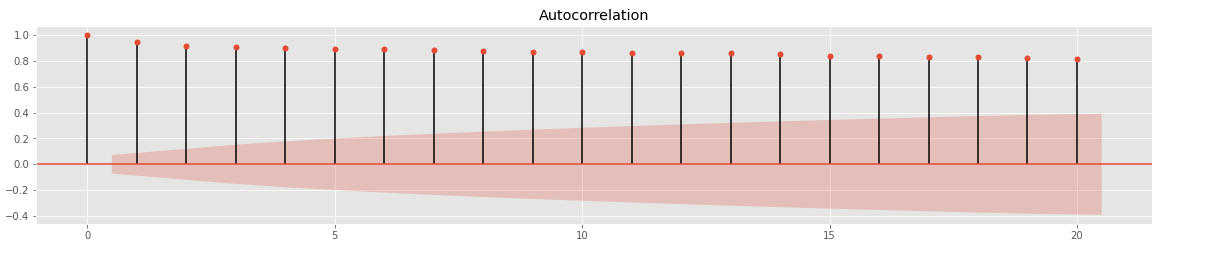
X축의 빨간색 범위를 벗어나 있으면 Autocorrelation이 있다고 판단
=> 정상성 X
3. Dickey-Fuller Test
귀무가설: 정상성 x
대립가설: 정상성 o
# adfuller library
from statsmodels.tsa.stattools import adfuller
# check_adfuller
def check_adfuller(ts):
# Dickey-Fuller test
result = adfuller(ts, autolag='AIC')
print('Test statistic: ' , result[0])
print('p-value: ' ,result[1])
print('Critical Values:' ,result[4])검정 결과

Q7. p-value 값이 0.577~이다. 정상성이 있는걸까 없는걸까? (귀무가설을 기각하지 못하여 정상성이 없다고 할수있다)
4. Rolling statisitcs
N일간의 평균과 표준편차(분산)을 구해 값이 일정한지 파악
# check_mean_std
def check_mean_std(ts):
#Rolling statistics
rolmean = ts.rolling(6).mean()
rolstd = ts.rolling(6).std()
plt.figure(figsize=(22,10))
orig = plt.plot(ts, color='red',label='Original')
mean = plt.plot(rolmean, color='black', label='Rolling Mean')
std = plt.plot(rolstd, color='green', label = 'Rolling Std')
plt.xlabel("Date")
plt.ylabel("Mean Temperature")
plt.title('Rolling Mean & Standard Deviation')
plt.legend()
plt.show()
# check stationary: mean, variance(std)and adfuller test
check_mean_std(ts)
check_adfuller(ts.MeanTemp)시각화

표준편차(분산)은 일정한 크기를 가진 패턴인데, 평균은 여전히 비정상성을 보여준다.
(5) 비정상성 해결하기
1.Moving average method
window_size = 6
moving_avg = ts.rolling(window_size).mean()
plt.figure(figsize=(22,10))
plt.plot(ts, color = "red",label = "Original")
plt.plot(moving_avg, color='black', label = "moving_avg_mean")
plt.title("Mean Temperature of Bindukuri Area")
plt.xlabel("Date")
plt.ylabel("Mean Temperature")
plt.legend()
plt.show()
#기존 값-rolling mean
ts_moving_avg_diff = ts - moving_avg
ts_moving_avg_diff.dropna(inplace=True) # first 6 is nan value due to window size
# check stationary: mean, variance(std)and adfuller test
check_mean_std(ts_moving_avg_diff)
check_adfuller(ts_moving_avg_diff.MeanTemp)
결과
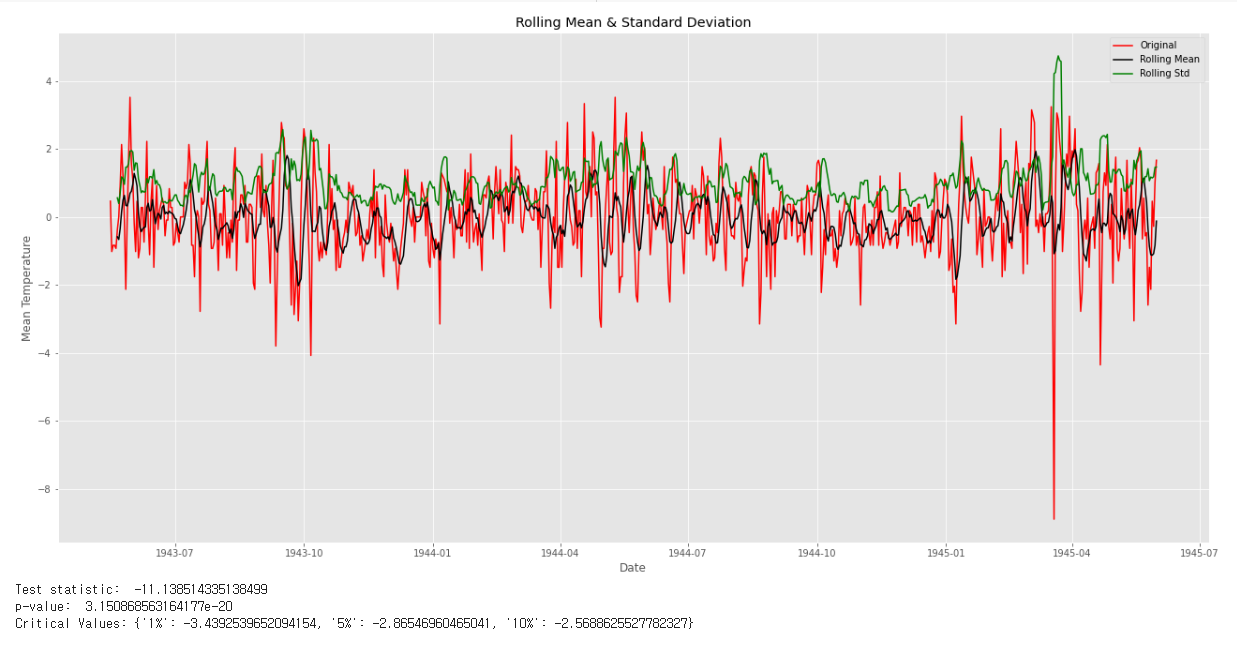
rolling mean과 std가 일정한 크기를 가진 패턴을 보여주고, Dickey-Fuller Test 결과, 귀무가설이 기각되어 정상성이 있음을 확인할 수 있다.
2. Differencing method
# differencing method
ts_diff = ts - ts.shift()
plt.figure(figsize=(22,10))
plt.plot(ts_diff)
plt.title("Differencing method")
plt.xlabel("Date")
plt.ylabel("Differencing Mean Temperature")
plt.show()
ts_diff.dropna(inplace=True) # due to shifting there is nan values
# check stationary: mean, variance(std)and adfuller test
check_mean_std(ts_diff)
check_adfuller(ts_diff.MeanTemp)
rolling mean과 std가 일정한 크기를 가진 패턴을 보여주고, Dickey-Fuller Test 결과, 귀무가설이 기각되어 정상성이 있음을 확인할 수 있다.
(6) 예측하기
Differencing method를 사용하여 정상성을 만들어주고
ARIMA 모델을 사용하여 예측
1. ARIMA(p,d,q) 에서 p,d,q 값 구하기
d의 경우 차분횟수를 뜻하며 d=1이 됨
p,q는 pacf와 acf의 그래프를 그린 후 파악

2. ACF와 PACF 그래프 그리기
# ACF and PACF
import statsmodels.api as sm
fig=plt.figure(figsize=(20,8))
ax1=fig.add_subplot(211)
fig=sm.graphics.tsa.plot_acf(ts_diff[1:],lags=20, ax=ax1)
ax2=fig.add_subplot(212)
fig=sm.graphics.tsa.plot_pacf(ts_diff[1:],lags=20, ax=ax2)결과
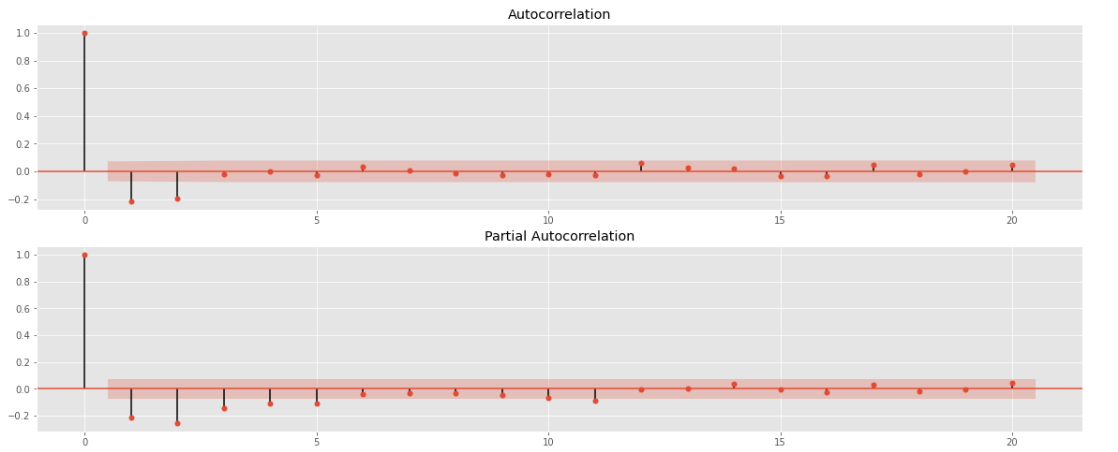
p, q = 1 or 2
ARIMA(2,1,2)를 베이스모델로, ARIMA(2,1,1), ARIMA(1,1,2), ARIMA(1,1,1) 등의 모델 시도 가능
3. Test set 분리
총 데이터: 1943년 5월 11일부터 1945년 5월 31일까지의 데이터 (751일)
Test data: 1944년 6월 25일부터 1945년 5월 31일(340일)
4. 모델 fitting 및 예측
총 4개의 모델에 대해 fitting
# ARIMA LİBRARY
from statsmodels.tsa.arima_model import ARIMA
from pandas import datetime
# fit model
model1 = ARIMA(ts, order=(2,1,2))
model2 = ARIMA(ts, order=(2,1,1))
model3 = ARIMA(ts, order=(1,1,2))
model4 = ARIMA(ts, order=(1,1,1))
start_index = datetime(1944, 6, 25)
end_index = datetime(1945, 5, 31)
#metrics 함수
from sklearn import metrics
def scoring(y_true, y_pred):
r2=round(metrics.r2_score(y_true, y_pred) * 100,3)
rmse=round(metrics.mean_squared_error(y_true, y_pred, squared=False), 3)
df=pd.DataFrame({'R2': r2, "RMSE":rmse},index=[0])
return df
####predict 할때 typ='levels'로 설정해야됨...차분이 들어간 모델의 경우 default인 linear로 설정하면 차분한 값에 대한 결과가 나오기 떄문
for i in range(1,5):
globals()['model{}_fit'.format(i)]=globals()['model{}'.format(i)].fit()
globals()['forecast{}'.format(i)]=globals()['model{}_fit'.format(i)].predict(start=start_index, end=end_index, typ='levels')
5. 성능 비교
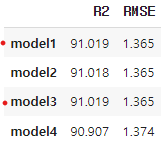
Model1(ARIMA(2,1,2)) 과 Model3(ARIMA(1,1,2)) 가 가장 좋음
6. Fitting된 ARIMA(2,1,2) 모델의 실제값과 예측값 비교
# visualization
plt.figure(figsize=(22,10))
plt.plot(weather_bin.Date,weather_bin.MeanTemp,label = "original")
plt.plot(forecast1,label = "predicted")
plt.title("Time Series Forecast")
plt.xlabel("Date")
plt.ylabel("Mean Temperature")
plt.legend()
plt.show()
얼추 비슷!
7. Fitting된 ARIMA(2,1,2) 모델의 잔차분석
resi=np.array(weather_bin[weather_bin.Date>=start_index].MeanTemp)-np.array(forecast1)
plt.figure(figsize=(22,8))
plt.plot(weather_bin.Date[weather_bin.Date>=start_index], resi)
plt.xlabel("Date")
plt.ylabel("Residual")
plt.legend()
plt.show()
특정한 패턴이 보이지 않는다. Random 하다.
#ACF 그래프도 확인
fig=plt.figure(figsize=(20,10))
ax1=fig.add_subplot(111)
fig=sm.graphics.tsa.plot_acf(resi,lags=20, ax=ax1)

잔차 역시 정상성을 가지고 있음을 확인할 수 있다.
끝~
'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열 스터디] ARIMA Code Reading (0) | 2022.11.25 |
|---|---|
| [시계열 스터디] ARIMA 모델 part5 (0) | 2022.11.13 |
| [시계열 스터디] ARIMA Model part6 (1) | 2022.11.13 |
| [시계열] ARIMA 모델 - Part 4 (0) | 2022.11.03 |
| [시계열 스터디] ARIMA Model part3 (0) | 2022.10.09 |





댓글 영역