고정 헤더 영역
상세 컨텐츠
본문
* 작성자 : 16기 박종혁
본 포스팅은 Kaggle <End to end Seasonal ARIMA electricity forecast>를 참고하여 작성되었습니다.
https://www.kaggle.com/code/janiezj/end-to-end-seasonal-arima-electricity-forecast
[ ARIMA Code Reading ]
0. About Data
해당 데이터는 1985년부터 2018년까지 매달 전기 소비율이다.
1. Split dataset
시계열 데이터를 학습하고 평가하기 위해 먼저 train data와 test data로 분리한다. 그 결과 train data 361개, test data 36개로 나누었다.
2. Explore Training Dataset
2.1 Visualize Data

- 전기 소비량이 시간에 따라 증가함을 알 수 있다. 그러나 최근 몇 년 간 감소 추세임을 예상할 수 있다.
- 매년 전기 소비량이 seasonality를 보이므로 정상성을 만족하지 않는다고 볼 수 있다. -> 차분 진행
- 시간이 지날수록 년도별 분산이 증가함을 알 수 있다(데이터 변형 고려 가능).

보다 자세히 년도별 변화 추이를 살펴본 결과, 4월과 10월에는 낮은 수치를 보이고 8월과 12월에는 높은 수치를 보인다. 이러한 양상은 매해 비슷하게 나타난다. 즉 해당 데이터는 강한 seasonality를 나타내 있다.
2.2 Check Temporal Structure
시계열의 기본 패턴을 개별 성분으로 분해하여 시계열의 특성을 분석하고, 이 분해한 성분을 분석한 후 다시 합쳐서 전체적인 시계열을 예측하는 방법이 분해법이다.
해당 시계열 데이터를 분해하는 방법에는 크게 두 가지가 존재한다. 바로 가법을 적용한 분해법과 승법을 적용한 분해법이다. 일반적으로 원본 데이터가 일정하게 안정적인 그래프를 그린다면 가법, 증가하거나 감소하는 형태를 띈다면 승법을 적용한 분해법을 선택한다.
가법을 적용한 분해법 -> [Raw data = Trend + Seasonal + 불규칙]
승법을 적용한 분해법 -> [Raw data = Trend * Seasonal * 불규칙]

승법을 이용하여 분해한 경우 seasonal 패턴과 trend가 보인다. 그러나 residual을 살펴보면 1 근처에 분포되어 있으므로 해당 분해법은 정확하지 않다고 할 수 있다(너무 작은 표준편차를 띄고 있다).
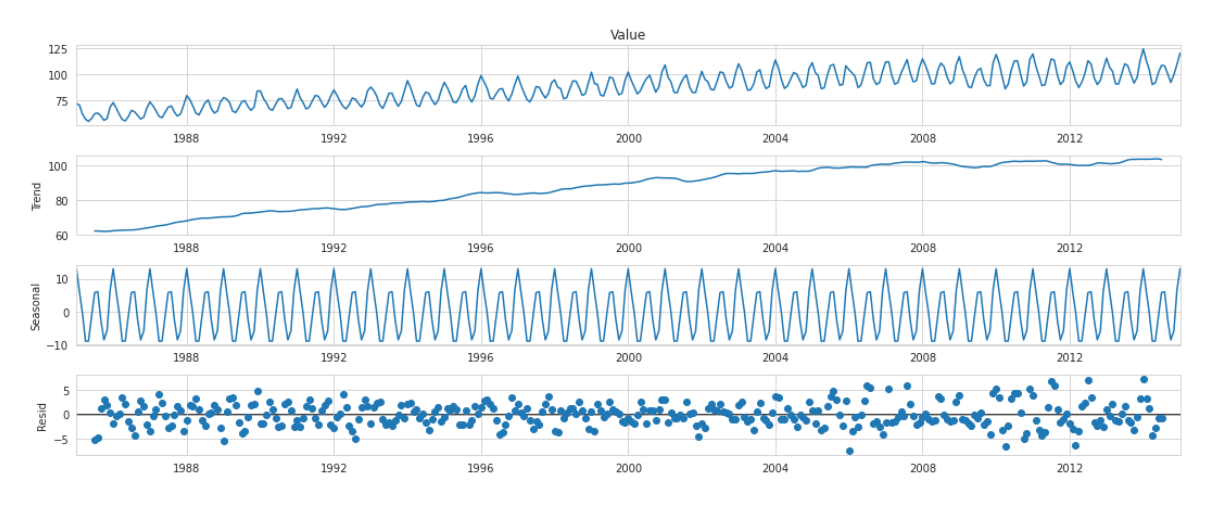
가법을 이용하여 분해한 경우 역시 seasonal 패턴과 trend가 보인다. 이번에도 residual을 살펴보면 승법을 이용한 분해와 달리 0근처에 특정한 패턴을 띄지 않고 분포되어 있으므로 적절하다고 볼 수 있다.
2.3 Stationarity
정상성의 유무를 확인하기 위해 통계적인 방법을 사용하고자 한다. 바로 Augmented Dickey-Fuller Test이다. 이 때 귀무가설은 데이터가 정상성을 만족하지 않는다는 것이고 대립 가설은 정상성을 만족한다는 것이다.
H0 : It is non stationarity Ha : It is stationarity.

p-value가 0.05보다 크므로 귀무가설을 기각하지 못하고 정상성을 만족하지 않는다고 볼 수 있다. 따라서 정상성을 만족하기 위해 차분을 진행한다.
## Augmented Dickey-Fuller Test란?
정상성을 흔히 그림을 통해 시각적으로 판단할 수 있지만 보다 정량적으로 검증할 수 있는 방법

이 때 과거 데이터 앞에 곱해져 있는 a를 기준으로 정상성을 판단할 수 있다. 직관적으로 설명하면 과거값의 영향이 피드백되어 현재 값에 영향을 주므로 전체 과거의 영향이 1이하가 되어야 데이터가 발산하지 않게 되고 정상성을 띄게 된다.
[보다 자세한 내용은 https://blog.naver.com/deniro33/222850888571 를 참고]
2.4 Differencing
현재 데이터는 강한 seasonality와 trend가 존재하기 때문에 정상성을 만족시키기 위해 seasonal differencing을 진행한다. 즉 data를 12만큼 lag하여 차분을 진행한다.

다시 한 번 Augmented Dickey-Fuller Test를 진행한 결과 귀무가설을 기각하고 정상성을 만족한다고 볼 수 있다.
2.5 ACF & PACF

- 위의 두 그래프를 보면 ACF 그래프는 2 시점 이후에 급격히 감소함을 알 수 있다. PACF 그래프 또한 2 시점 이후에 급격히 감소함을 알 수 있다. 따라서 비계절적 요인은 (0,0,2) 혹 (2,0,0)으로 구성할 수 있다.
- Seasonal component를 고려하면 한 시즌이 끝난 후, 즉 lag가 12 직후에 급격히 감소함을 알 수 있다. 따라서 seasonal component 입장에서는 (0,1,1,12)로 구성할 수 있다.
- 이를 바탕으로 비슷한 다양한 모델들을 확인해본 결과 SARIMA(2,0,2)(0,1,1,12) 모델이 가장 작은 RMSE 값을 가진다.
3. Evaluate Models
3.1 Evaluate manually configured SARIMA model
앞서 기술한 대로 SARIMA(2,0,2)(0,1,1,12) 모델을 설정한다. 그리고 RMSE를 파악한다.

구한 결과 RMSE는 3.689로 나타난다. 이 후 residual을 분석하여 모델이 적절한지 파악한다.

- Residual Autocorrelation Plot을 보면 특별한 패턴이 발견되지 않는다.
- Residual Line Plot을 보면 0 근처에 random하게 분포되어 있기 때문에 큰 문제가 없다.
- Residual Q-Q plot을 보면 꽤 정규분포를 따름을 알 수 있다.
- Histogram을 살펴보면 정규분포와 꽤 비슷함을 알 수 있다.
3.2 Evaluate Automated Model Selection

pmdarima 라이브러리를 사용하여 가장 적합한 모델을 자동으로 찾는 과정을 수행한다.

그 결과 SARIMAX(1,1,2)(2,0,2,12) 모델이 선정되었다.
구한 결과 RMSE는 4.486으로 나타난다. 이 후 residual을 분석하여 모델이 적절한지 파악한다.

잔차 분석을 진행한 결과 모델이 적합함을 알 수 있다.
3.3 Compare RMSE
Manually configured model SARIMA(2,0,2)(0,1,1,12)의 RMSE는 3.689이고 Automated selected model SARIMA(1,1,2)(2,0,2,12)의 RMSE는 4.486이다. 따라서 Manually configured model SARIMA(2,0,2)(0,1,1,12)를 선택하는 것이 바람직하다.
'심화 스터디 > 시계열' 카테고리의 다른 글
| [시계열 스터디] 코드리뷰(1) (0) | 2022.11.24 |
|---|---|
| [시계열 스터디] ARIMA 모델 part5 (0) | 2022.11.13 |
| [시계열 스터디] ARIMA Model part6 (1) | 2022.11.13 |
| [시계열] ARIMA 모델 - Part 4 (0) | 2022.11.03 |
| [시계열 스터디] ARIMA Model part3 (0) | 2022.10.09 |





댓글 영역